Question

What is the minimum distance between the curve ${{y}^{2}}=4x$ and ${{x}^{2}}+{{y}^{2}}-12x+31=0$ ?
(a) $\sqrt{21}$
(b) $\sqrt{26}-\sqrt{5}$
(c) $\sqrt{20}-\sqrt{5}$
(d) $\sqrt{28}-\sqrt{5}$

Answer 1

To solve this problem we will suppose a point P at parabola in the form of $\left( {{t}^{2}},2t \right)$ and then we will assume the normal of the parabola at this point as $y+tx=2t+{{t}^{3}}$. After that we will draw the diagram of both the figures and we will find out that for minimum distance this normal has to pass through the centre of the circle i.e. (6, 0), using this condition we will find the out the point P and then using distance formula we will calculate the distance between centre of the circle and point P and then subtract radius from it to get the shortest distance.

Complete step by step answer:
We are given two curves ${{y}^{2}}=4x$ and ${{x}^{2}}+{{y}^{2}}-12x+31=0$,
And we have to find the shortest distance between these curves,
First of all we will draw diagram for these curves,
We have equation of a circle as ${{x}^{2}}+{{y}^{2}}-12x+31=0$
Here centre = $\left( \dfrac{12}{2},0 \right)=\left( 6,0 \right)$
And radius = $\sqrt{{{6}^{2}}+{{0}^{2}}-31}=\sqrt{5}$
So figure of the given curves is as follows,

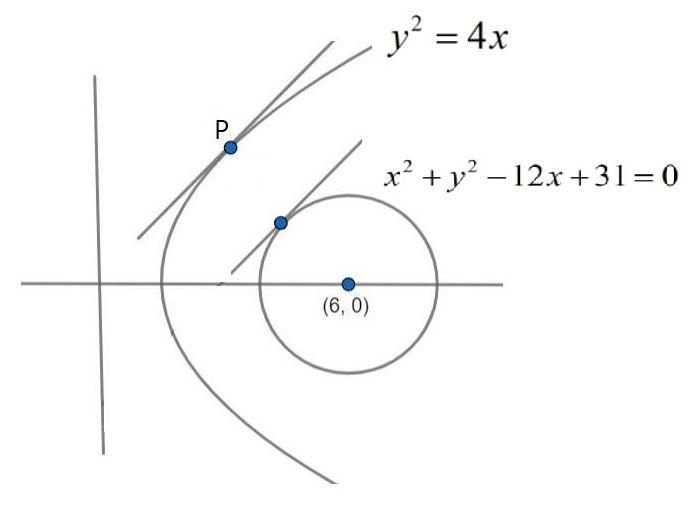
In this figure we will assume the parametric coordinates of the point P as $\left( {{t}^{2}},2t \right)$,
We can see form the figure that the minimum distance is between the points at which tangent to both curves are parallel to each other so the normal at point P will pass through the centre of the given circle i.e. through (6, 0).
And we know that equation of the normal through a point $\left( {{t}^{2}},2t \right)$ for parabola ${{y}^{2}}=4x$ is given by,
$y+xat=2at+a{{t}^{3}}$
And in the parabola ${{y}^{2}}=4x$, a = 1 so we get
$y+tx=2t+{{t}^{3}}$
Now this above equation passes through point (6, 0) hence it should satisfy this point,
So by putting x = 6 and y = 0, we get
$y+tx=2t+{{t}^{3}}$
$0+6t=2t+{{t}^{3}}$
${{t}^{3}}-4t=0$
Taking t as common, we get

& t\left( {{t}^{2}}-4 \right)=0 \\\ & t\left( t-2 \right)\left( t+2 \right)=0 \\\ \end{aligned}$$ We get three values of t as, $t=0,2,-2$ So point $\left( {{t}^{2}},2t \right)$, can be, $\left( 0,0 \right),\left( 4,-4 \right),\left( 4,4 \right)$ Now using the distance formula we will calculate the distance between these points and the centre of the circle, Point (0,0) $\sqrt{{{\left( 6-0 \right)}^{2}}+{{\left( 0-0 \right)}^{2}}}=6$ Point (4,-4) $\sqrt{{{\left( 6-4 \right)}^{2}}+{{\left( 0-\left( -4 \right) \right)}^{2}}}=\sqrt{4+16}=\sqrt{20}$ Point (4,4) $\sqrt{{{\left( 6-4 \right)}^{2}}+{{\left( 0-\left( 4 \right) \right)}^{2}}}=\sqrt{4+16}=\sqrt{20}$ Hence minimum distance is from point (4,-4) or from (4,4) Now according to figure to find minimum distance between curves we will have to subtract radius from it, so we get minimum distance as, $\begin{aligned} & \sqrt{20}-radius \\\ & =\sqrt{20}-\sqrt{5} \\\ \end{aligned}$ **So, the correct answer is “Option C”.** **Note:** To solve this problem you need to have the basic prior knowledge about parabola and circle i.e. how to calculate the equation of normal to a parabola and how to assume points in the parametric form of parabola etc. Otherwise you won’t be able to solve this problem without these prior concepts, so go through all of these basic concepts to solve these kinds of problems.