Question

What is the midpoint of the line segment joining the points $(2,\ 1)$ and $( - 1,\ 4)$ ?

Answer 1

In this question, we need to find the midpoint of the line segment joining the points $(2,\ 1)$ and $( - 1,\ 4)$. Midpoint is nothing but the middle point of the line segment that divides it into two equal parts. Let us consider the given points as A and B and also the midpoint of the two points as M. There is a direct formula to find the midpoint of the two points. Then by using the formula of midpoint and simplifying , we can find the midpoint.

Complete step by step solution:
In the figure, AB is a line segment in the XY plane ( as the mentioned coordinates lie on the x and y axis) and $M(x,\ y)$ is the middle point of the line AB.

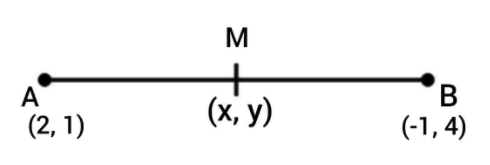
The middle point of any two points $\left( x_{1},\ y_{1} \right)$ and $\left( x_{2},\ y_{2} \right)$ is $\left( \dfrac{x_{1} + x_{2}}{2},\dfrac{y_{1} + y_{2}}{2} \right)$
Given $(2,\ 1)$ and $( - 1,\ 4)$
Here we need to find the midpoint of the line segment joining the points $(2,\ 1)$ and $( - 1,\ 4)$.
Let us consider the points be $A$ and $B$. $A$ be $\left( x_{1},\ y_{1} \right)$ where $x_{1}$ is $2$ and $y_{1}$ is $1$ . $B$ be $\left( x_{2},\ y_{2} \right)$ where $x_{2}$ is $- 1$ and $y_{2}$ is $4$ .
We know that middle point is half the sum of initial and final points of the line segment for their respective axis which is given by,
$\left( x,y \right) = \left( \dfrac{x_{1} + x_{2}}{2},\dfrac{y_{1} + y_{2}}{2} \right)$
Now on substituting values,
We get,
$M = \left( x,\ y \right) = \left( \dfrac{2 + \left( - 1 \right)}{2},\dfrac{1 + 4}{2} \right)$
On simplifying,
We get,
$M = \left( \dfrac{2 – 1}{2},\dfrac{5}{2} \right)$
On further simplifying,
We get,
$M = \left( \dfrac{1}{2},\dfrac{5}{2} \right)$
Thus we get the mid point of the line segment joining the points $(2,\ 1)$ and $( - 1,\ 4)$ is $\left( \dfrac{1}{2},\dfrac{5}{2} \right)$
The mid point of the line segment joining the points $(2,\ 1)$ and $( - 1,\ 4)$ is $\left( \dfrac{1}{2},\dfrac{5}{2} \right)$ .

Note:
This is a direct question but still we may make mistake by writing the wrong formula of the midpoint that is we may write it as $\left( \dfrac{x_{1} – x_{2}}{2},\dfrac{y_{1} – y_{2}}{2} \right)$ . We need to enclose negative terms in brackets to avoid calculation mistakes. While opening the brackets make sure that we are opening the brackets properly with their respective signs. The midpoint is nothing but a centre or midpoint of a line segment.