Question

What is the maximum volume of the box for the parameters given below:
Given, a rectangular sheet of cardboard, 16in. by 10in. . You are asked to cut-off identical squares from each of the four corners of the sheet and then bend up the sides of the remaining cardboard to form a rectangular box.

Answer 1

We will assume the length of square to be a certain variable. Then we will see the new parameters of the piece of cardboard sheet left with us and write the volume of the cardboard sheet in terms of the assumed length. This will give us a function which will give us the volume of the rectangular box so formed. Maximizing this function will give us the maximum volume of the box.

Complete step by step answer:
Let us assume the length of the square to be cut from each side is ‘x’. Then, we can understand the resulting cardboard sheet with the help of the following diagram:

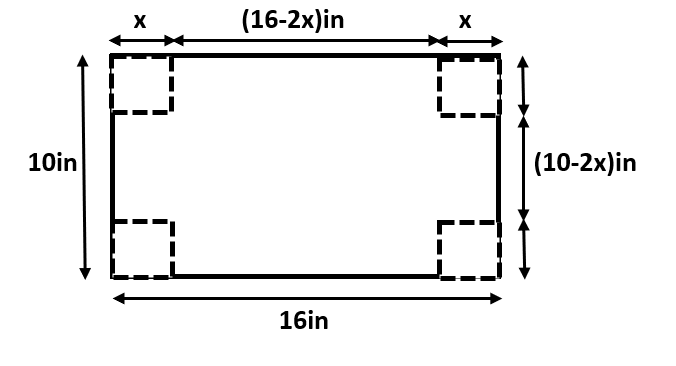
Thus, for the remaining section of our cardboard, we have:
length is equal to: $\left( 16-2x \right)in$
length is equal to: $\left( 10-2x \right)in$
Now, there will be two cases. First, when we make a cuboid by straightening the $\left( 10-2x \right)in$flap and second, when we make a cuboid by straightening the $\left( 16-2x \right)$ flap.
In the first case, we have the volume as:
$\begin{aligned} & \Rightarrow {{V}_{1}}=\left( 16-2x \right)\times 10\times x \\\ & \Rightarrow {{V}_{1}}=160x-20{{x}^{2}} \\\ \end{aligned}$
Now, to get the maxima of this volume, we have:
$\begin{aligned} & \Rightarrow \dfrac{d{{V}_{1}}}{dx}=0 \\\ & \Rightarrow \dfrac{d\left[ 160x-20{{x}^{2}} \right]}{dx}=0 \\\ & \Rightarrow 160-40x=0 \\\ & \therefore x=4 \\\ \end{aligned}$
Therefore, for $x=4$, we get the volume as:
$\begin{aligned} & \Rightarrow {{V}_{1}}={{\left[ 160x-20{{x}^{2}} \right]}_{x=4}} \\\ & \Rightarrow {{V}_{1}}=\left( 640-320 \right)i{{n}^{3}} \\\ & \therefore {{V}_{1}}=320i{{n}^{3}} \\\ \end{aligned}$
In the second case, we have the volume as:
$\begin{aligned} & \Rightarrow {{V}_{2}}=\left( 10-2x \right)\times 16\times x \\\ & \Rightarrow {{V}_{2}}=160x-32{{x}^{2}} \\\ \end{aligned}$
Now, to get the maxima of this volume, we have:
$\begin{aligned} & \Rightarrow \dfrac{d{{V}_{2}}}{dx}=0 \\\ & \Rightarrow \dfrac{d\left[ 160x-32{{x}^{2}} \right]}{dx}=0 \\\ & \Rightarrow 160-64x=0 \\\ & \therefore x=\dfrac{5}{2} \\\ \end{aligned}$
Therefore, for $x=\dfrac{5}{2}$, we get the volume as:
$\begin{aligned} & \Rightarrow {{V}_{1}}={{\left[ 160x-32{{x}^{2}} \right]}_{x=\dfrac{5}{2}}} \\\ & \Rightarrow {{V}_{1}}=\left( 400-200 \right)i{{n}^{3}} \\\ & \therefore {{V}_{1}}=200i{{n}^{3}} \\\ \end{aligned}$
Therefore, on comparing the two volumes obtained, we see that the volume in the first case is greater. Thus the maximum volume could be $320i{{n}^{3}}$.
Hence, the maximum volume of the box for the given parameters comes out to be $320i{{n}^{3}}$.

Note: While solving our problem, we should be careful if the differential is giving a maxima or minima. Since, the functions for our volume expression were both decreasing quadratic, the point of zero differential was automatically a maxima. We should take note of these points while solving a problem of maxima and minima.