Question

What is the mass of inertia about AB axis?

A. $\dfrac{2}{3}m{{l}^{2}}$
B. $\dfrac{4}{3}m{{l}^{2}}$
C. $\dfrac{3}{2}m{{l}^{2}}$
D. $\dfrac{3}{4}m{{l}^{2}}$

Answer 1

Here we are talking about the moment of inertia which is defined by the rotation of a particle through its axis and we use the formula of moment of inertia that can be found by taking the product of mass and the square of the radius. The SI unit of moment of inertia is $kg{{m}^{2}}$.

Complete step by step solution:
As In the above question it is asked in the moment of inertia about AB axis, though it is mentioned in the above diagram that three masses each of mass M are placed at the corners of an equilateral triangle of side ‘$l$ ‘. Then the moment of inertia of this system along AB of the triangle.

If we rotate the side we find the moment of inertia which is denoted by ‘$I$ ‘ but we cannot not rotate the base of a triangle so that we can rotate the AB axis.

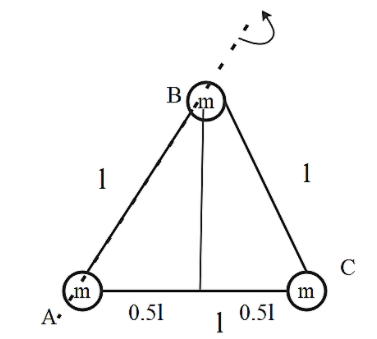
We make a perpendicular through point A and the mid point of AC is point P as the side is of length $l$so that the length of PC is $\dfrac{l}{2}$.

And now by using the pythagoras theorem in $\Delta APC$, we can find the distance AP
Such that,
$\Rightarrow {{(AP)}^{{{2}^{{}}}}}+{{(PC)}^{2}}={{(AC)}^{2}}$
$\Rightarrow {{(AP)}^{2}}+\dfrac{{{l}^{2}}}{4}={{l}^{2}}$
$\Rightarrow {{(AP)}^{2}}={{l}^{2}}-\dfrac{{{l}^{2}}}{4}$
$\Rightarrow {{(AP)}^{2}}=\dfrac{4{{l}^{2}}-{{l}^{2}}}{4}$
$\Rightarrow {{(AP)}^{2}}=\dfrac{3{{l}^{2}}}{4}$
$\Rightarrow AP=\dfrac{\sqrt{3}}{2}l$

As we know that the moment of inertia may be defined as,
$\Rightarrow I=M{{r}^{2}}$

Where M is the mass and r is the distance AP.
$\Rightarrow I=M\times {{(\dfrac{\sqrt{3}}{2}l)}^{2}}$
$\Rightarrow I=\dfrac{3}{4}M{{l}^{2}}$

Hence option (D) is the correct option.

Note:
One question arises in our mind that why we draw a perpendicular through point A and the reason behind it is that we have to find the radius. The moment of inertia is also known as mass of inertia, angular mass of inertia or rotational inertia.