Question

What is the magnitude of the net magnetic field at S.

& \text{A) 4}\text{.1}\times \text{1}{{\text{0}}^{-6}}T \\\ & \text{B) 1}\text{.6}\times \text{1}{{\text{0}}^{-6}}T \\\ & \text{C) 3}\text{.2}\times \text{1}{{\text{0}}^{-6}}T \\\ & \text{D) 2}\text{.1}\times \text{1}{{\text{0}}^{-6}}T \\\ \end{aligned}$$

Answer 1

We are given magnetic fields and currents through different which are mutually perpendicular to each other in a system. We can use Biot-Savart’s law to get the resultant magnitude of the magnetic field at the point S due to these fields.

Complete step-by-step solution:
Let us consider the given system. It consists of two different currents and the magnetic fields related to each of the currents. It is also given that the direction of the magnetic fields is perpendicular to each other, i.e., one is into the plane of the paper, and the other is outwards. We have to find the resultant magnetic field at point S due to these two fields at points P and Q. We can use Biot-Savart’s law to find the magnetic field due to the points P and Q as –
$B=\dfrac{{{\mu }_{0}}I}{2\pi r}$
Where, r is the distance from the point P to S or Q to S,
“I” is the current in the respective points.

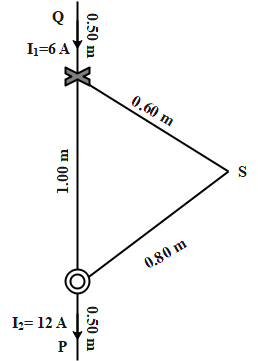
Let us find the magnetic field at S due to P –

& {{B}_{p}}=\dfrac{{{\mu }_{0}}{{I}_{2}}}{2\pi {{r}_{2}}} \\\ & \text{but, } \\\ & {{r}_{2}}=0.8m \\\ & {{I}_{2}}=2A \\\ & \Rightarrow {{B}_{p}}=\dfrac{{{\mu }_{0}}2}{2\pi (0.8)}\text{ } \\\ & \Rightarrow {{\text{B}}_{p}}\text{=}\dfrac{{{\mu }_{0}}}{0.8\pi }\text{--(1)} \\\ \end{aligned}$$ The magnetic field at S due to Q is given as – $$\begin{aligned} & {{B}_{Q}}=\dfrac{{{\mu }_{0}}{{I}_{1}}}{2\pi {{r}_{1}}} \\\ & \text{but, } \\\ & {{r}_{1}}=0.6m \\\ & {{I}_{1}}=6A \\\ & \Rightarrow {{B}_{Q}}=\dfrac{{{\mu }_{0}}6}{2\pi (0.6)}\text{ } \\\ & \Rightarrow {{\text{B}}_{Q}}\text{=}\dfrac{5{{\mu }_{0}}}{\pi }\text{--(2)} \\\ \end{aligned}$$ Now, we can easily find the resultant magnetic field using the equation to find the resultant of two quantities as – $$B=\sqrt{{{B}_{1}}^{2}+{{B}_{2}}^{2}+2{{B}_{1}}{{B}_{2}}\cos \theta }$$ But we know the two fields are perpendicular to each other. So, we get the resultant magnetic field at S as – $$\begin{aligned} & B=\sqrt{{{B}_{1}}^{2}+{{B}_{2}}^{2}+2{{B}_{1}}{{B}_{2}}\cos \theta } \\\ & \text{but,} \\\ & \theta \text{=9}{{\text{0}}^{0}} \\\ & \cos \theta =0 \\\ & \Rightarrow B=\sqrt{{{B}_{p}}^{2}+{{B}_{Q}}^{2}} \\\ & \Rightarrow B=\sqrt{{{(\dfrac{{{\mu }_{0}}}{0.8\pi })}^{2}}+{{(\dfrac{5{{\mu }_{0}}}{\pi })}^{2}}} \\\ & \Rightarrow B=\dfrac{{{\mu }_{0}}}{\pi }\sqrt{{{(\dfrac{5}{4})}^{2}}+{{5}^{2}}} \\\ & \Rightarrow B=\dfrac{{{\mu }_{0}}}{4\pi }\sqrt{25+400} \\\ & \Rightarrow B={{10}^{-7}}\sqrt{425}T \\\ & \Rightarrow B=2.06\times {{10}^{-6}}T \\\ \end{aligned}$$ The magnetic field at the point S due to the fields at the points P and Q is $$B=2.06\times {{10}^{-6}}T$$. This is the required solution. **The correct answer is option D.** **Note:** The magnetic field like the electric field can have only one direction and magnitude at a given point. This is why we need to calculate the resultant magnitude using the vector method. The magnetic field is unidirectional at a given point by interacting with other fields.