Question

What is the locus of the mid-point of the chord of contact of tangents drawn from points lying on the straight line $4x - 5y = 20$ to the circle ${x^2} + {y^2} = 9$?
(a). $20({x^2} + {y^2}) - 36x + 45y = 0$
(b). $20({x^2} + {y^2}) + 36x - 45y = 0$
(c). $20({x^2} + {y^2}) - 20x + 45y = 0$
(d). $20({x^2} + {y^2}) + 20x - 45y = 0$

Answer 1

Hint: Determine the tangent and the chord of contact of the tangents from the point (h, k) that lies of the line $4x - 5y = 20$. Assume (a, b) to be the midpoint of the chord. Find the relation between a and b, and replace a and b with x and y respectively.

Complete step-by-step answer:

We need to find the locus of the mid-point of the chord of contact of tangents drawn from points lying on the straight line $4x - 5y = 20$ to the circle ${x^2} + {y^2} = 9$.

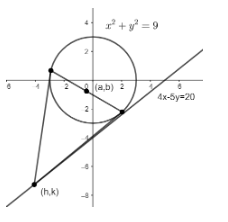
Consider a point (h, k) on the line $4x - 5y = 20$, then, we have:
$4h - 5k = 20.............(1)$
The equation of chord of contact of the tangents to the circle ${x^2} + {y^2} = 9$ from a point (a, b) outside the circle is given by:
$ax + by = 9$
The equations of chord of contact of the tangents from the point (h, k) to the circle ${x^2} + {y^2} = 9$ is then given as follows:
$hx + ky = 9..........(2)$
Let (a, b) be the mid-point of the chord of contact of the tangents.
Then, the equation of the chord with the midpoint (a, b) is given as follows:
$ax + by = {a^2} + {b^2}..........(3)$
Line in equation (2) and equation (3) are the same. Hence, we have:
$\dfrac{h}{a} = \dfrac{k}{b} = \dfrac{9}{{{a^2} + {b^2}}}$
The value of h in terms of a and b is given by:
$h = \dfrac{{9a}}{{{a^2} + {b^2}}}..........(4)$
The value of k in terms of a and b is given by,
$k = \dfrac{{9b}}{{{a^2} + {b^2}}}..........(5)$
Substituting equations (4) and (5) in equation (1), we have:
$4\left( {\dfrac{{9a}}{{{a^2} + {b^2}}}} \right) - 5\left( {\dfrac{{9b}}{{{a^2} + {b^2}}}} \right) = 20$
Simplifying, we get:
$36a - 45b = 20({a^2} + {b^2})$
$20({a^2} + {b^2}) - 36a + 45b = 0$
Replacing a and b with x and y respectively, we get:
$20({x^2} + {y^2}) - 36x + 45y = 0$
Hence, the correct answer is option (a).

Note: The equation of the chord with a midpoint (a, b) is $ax + by = {a^2} + {b^2}$. The equation of the chord of contact of tangents drawn from the point (h, k) outside the circle ${x^2} + {y^2} = {a^2}$ is $hx + ky = {a^2}$.