Solveeit Logo
Login

Question

Question: What is the line equation that has \[x-\] intercept \[=4\] and \[y\]\[-\] intercept \[=-5\]?...

What is the line equation that has x−x- intercept =4=4 and y$$$$- intercept =−5=-5?

Explanation

Solution

In order to find the line equation, firstly we will be considering the general line equation i.e. y=mx+cy=mx+c and then we will be determining the value of cc and from that we will be determining the value of mm which is the slope. And upon solving, we will be solving the obtained equations and we will get the equation of line required.

Complete step by step solution:
Now let us learn about the line equations. The general line equation is of the form y=mx+cy=mx+c where, mm is the slope and cc is the y$$$$- intercept. There are three major forms of line equations. They are: point-slope form, standard from and slope-intercept form.
Now let us start finding out the line equation that has x−x- intercept =4=4 and y$$$$- intercept =−5=-5.
Let us consider the equation y=mx+cy=mx+c.
Now we will be determining the value of cc.
As the x−axisx-axis crosses the y−axisy-axis at x=0x=0, we will be substituting 00 for xx.
We get,
y=m(0)+cy=m\left( 0 \right)+c
Upon solving, we get, y=cy=c.
From the given question, we have that y$$$$-intercept=−5=-5. Since y=cy=c, we can state that c=−5c=-5.
Now consider y=mx+cy=mx+c
Then we get, y=mx−5y=mx-5
Now, let us determine the value of mm i.e. slope.
m=change in ychange in xm=\dfrac{\text{change in y}}{\text{change in x}}
Now let us determine the intercepts into the points.
For y$$$$- intercept, we have P1(x1,y1){{P}_{1}}\left( {{x}_{1}},{{y}_{1}} \right) i.e. (0,−5)\left( 0,-5 \right).
For x−x- intercept, we have P2(x2,y2){{P}_{2}}\left( {{x}_{2}},{{y}_{2}} \right) i.e. (4,0)\left( 4,0 \right).
\Rightarrow $$$$m=\dfrac{\text{change in y}}{\text{change in x}}$$$$=\dfrac{{{y}_{2}}-{{y}_{2}}}{{{x}_{2}}-{{x}_{1}}}$$$$=\dfrac{0-\left( -5 \right)}{4-0}=\dfrac{0+5}{4}=\dfrac{5}{4}
Now upon substituting the value of mm in the equation y=mx−5y=mx-5, we get the line equation as y=54x−5y=\dfrac{5}{4}x-5.
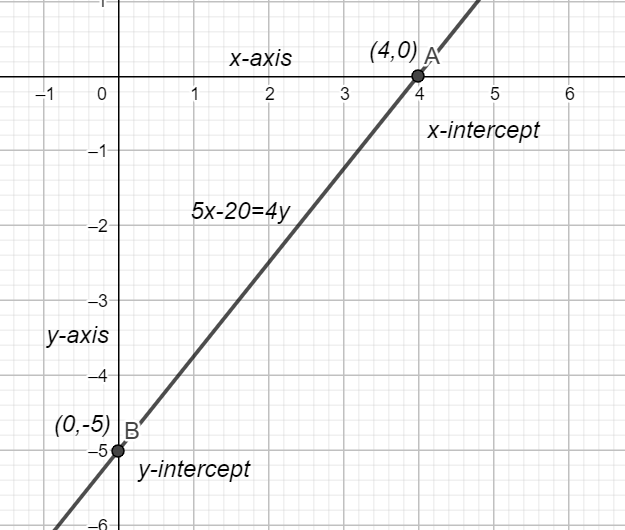
This can also be simplified and written as 4y=5x−204y=5x-20
∴\therefore The line equation that has x−x-intercept=4=4 and y$$$$-intercept=−5=-5 is 4y=5x−204y=5x-20.

Note: For a non vertical line, if it passes through (x0,y0)\left( x_0,y_0 \right) with the slope mm, then the equation of line would be y−y0=m(x−x0)y-y_0=m\left( x-x_0 \right).
Now let us plot our obtained line equation.