Question

What is the limit as x approaches infinity of $\dfrac{1}{x}$?

Answer 1

Here we will use the graphical method to determine the value of the limit. Assume the required limit as L. Now, to find the value of $\displaystyle \lim_{x \to \infty }\left( \dfrac{1}{x} \right)$, first draw the graph of the rectangular hyperbola $\dfrac{1}{x}$. Check the value of function as x tends to infinity. If this value is a finite number then that will be our answer.

Complete step by step answer:
Here we have been asked to find the limit of the function $\dfrac{1}{x}$ as the domain value, i.e. x, tends to infinity. Let us assume the limit value as L so mathematically we have,
$\Rightarrow L=\displaystyle \lim_{x \to \infty }\left( \dfrac{1}{x} \right)$
Now, let us find the limit value of the function using the graphical method. We can clearly see that the given function is an equation of a rectangular hyperbola. So, the graph of the rectangular hyperbola $f\left( x \right)=\dfrac{1}{x}$ can be shown as: -

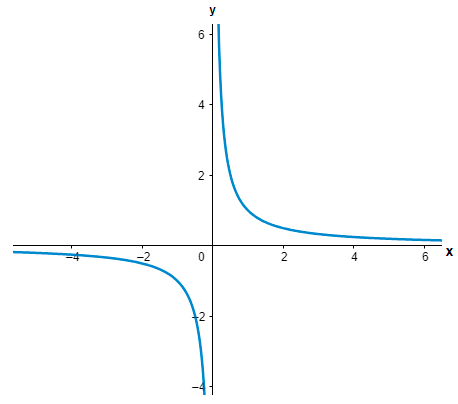
From the above graph we can see that as x tends to infinity, the value of the function tends to 0. So we have,
$\Rightarrow L=\left( \dfrac{1}{\infty } \right)=0$
Clearly 0 is a finite number, hence we can conclude that the limit of the given function is equal to 0.

Note: You must remember the graph of the rectangular hyperbola to solve the above question. Remember that infinity is not a real number so the value of x cannot be infinity exactly but only tends to infinity. Note that the function is not continuous at x = 0. In addition, also remember the graph of the functions like: $\ln x$, ${{e}^{x}}$, trigonometric and inverse trigonometric functions.