Question

What is the limit as x approaches infinity of ${{e}^{x}}$?

Answer 1

In this type of question we have to use the concept of limit at infinity. We know that the idea of a limit is the basis of all calculus. Also we know that, a limit tells us the value that the given function approaches as that function’s input approaches to some number.

Complete step by step answer:
In the given question, we have to find the limit of ${{e}^{x}}$ as $x$ approaches to $\infty$.
Hence, the function is $f\left( x \right)={{e}^{x}}$ and limit as $x$ approaches to $\infty$ i.e. $x \to \infty$
$\Rightarrow \displaystyle \lim_{x \to \infty }f\left( x \right)=\displaystyle \lim_{x \to \infty }{{e}^{x}}$
By applying the value of $x$ as $\infty$, we can write,
$\Rightarrow \displaystyle \lim_{x \to \infty }{{e}^{x}}={{e}^{\infty }}$
As we know that, the domain of ${{e}^{x}}$ is the whole of $\mathbb{R}$ and the range is $\left( 0,\infty \right)$. Also ${{e}^{x}}$ is continuous function defined on the whole of $\mathbb{R}$ and infinitely differentiable, with $\dfrac{d}{dx}{{e}^{x}}={{e}^{x}}$.
Hence, the value of ${{e}^{\infty }}=\infty$
$\Rightarrow \displaystyle \lim_{x \to \infty }{{e}^{x}}=\infty$
Thus, the limit as $x$ approaches $\infty$ of ${{e}^{x}}$ is $\infty$.

Note: In this type of question one of the students may state the result with the help of a graph also. The function $f\left( x \right)={{e}^{x}}$ is an equation in which the variable is an exponent, and the graph is exponentially increasing with respect to $x$. Where, $x$ is a real number and $e$ is a positive constant. The graph for $f\left( x \right)={{e}^{x}}$ is as follows:

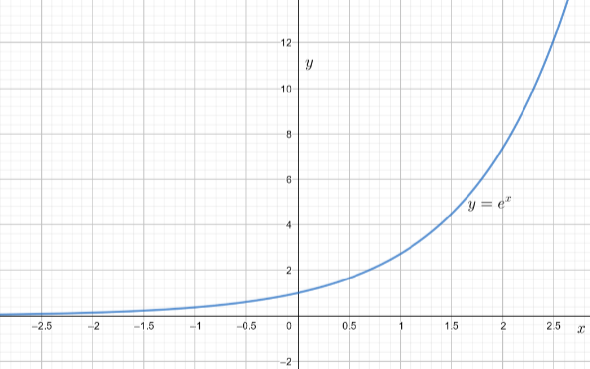
From the above graph of ${{e}^{x}}$ with respect to $x$ we can clearly observe that as $x$ approaches to $\infty$, the function ${{e}^{x}}$ also approaches to $\infty$.
Thus, the limit as $x$ approaches $\infty$ of ${{e}^{x}}$ is $\infty$.