Question
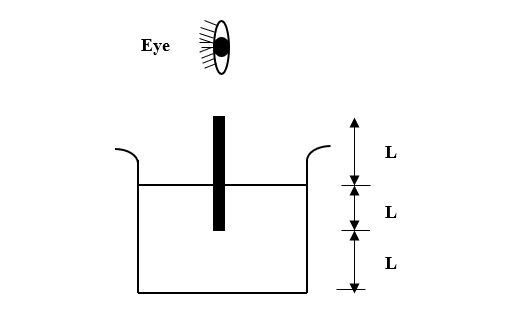
Question: What is the length of the image of the rod in the mirror, according to the observer in air? (Refract...
What is the length of the image of the rod in the mirror, according to the observer in air? (Refractive index of the liquid is μ).
A. μL+L
B. L+μL
C. Lμ+μL
D. None of these
Solution
To solve this problem first find the apparent depth of the rod which is dipped in the liquid. Then, find the apparent length of the rod. Then using the same formula, find the length of the rod when observed from air. Substitute the value for apparent length in the formula and find the real length of the rod. This obtained value will be the length of the image of the rod in the mirror, according to the observer in air.
Formula used:
μ=RealdepthApparentdepth
Complete answer:
Given: Refractive index of the liquid= μ
Length of the rod above liquid= Length of the rod dipped in the liquid= L
We know. relation between apparent depth and real depth is given by,
μ=RealdepthApparentdepth …(1)
Substituting the values in above equation we get,
μ=LApparentdepth
⇒Apparentdepth=μL
Thus, the apparent length of the rod will be given by,
L0=L+μL …(2)
Now, the length of the rod when seen from the air is given by,
μ=ReallengthApparentlength
Now, substituting the equation. (2) in above equation we get,
μ=ReallengthL+μL
Rearranging the above equation we get,
Reallength=μL+μL
⇒Reallength=μL+L
Hence, according to the observer in the air, the length of the image of the rod in the mirror is L+μL.
So, the correct answer is “Option B”.
Note:
Students must remember that when an observer is in a rarer medium and the object is in denser medium then the length of the immersed portion will be shorter. In this case, the real depth is always greater than the apparent depth. When the object is in a rarer medium and the observer is in a denser medium then the apparent depth is greater than the real depth. Example for this can be an aeroplane flying in the sky. It appears to us at a greater than its actual height when viewed from ground.
