Question

What is the impulse generated in the string subsequently?
A. $\dfrac{mu}{2}$
B. $\dfrac{mu}{4}$
C. $\dfrac{2mu}{3}$
D. $\dfrac{4mu}{3}$

Answer 1

Using the formula of momentum and impulse to derive the alternative formula for impulse. Further simplifying the equation with integration then comparing both end points of mass in string. Calculate further and then find out the impulse generated by reducing the impulse with compared impulse.

Complete step-by-step answer:
In the question, the force acting for a small-time had a great effect on the momentum on the other side of the string. A small force can make the same change in momentum, but it would have to act for a much longer time. For example, if the ball were thrown upward, the gravitational force would eventually reverse the momentum of the ball. Thus, the effect we are talking about is the change in momentum$\Delta p$.

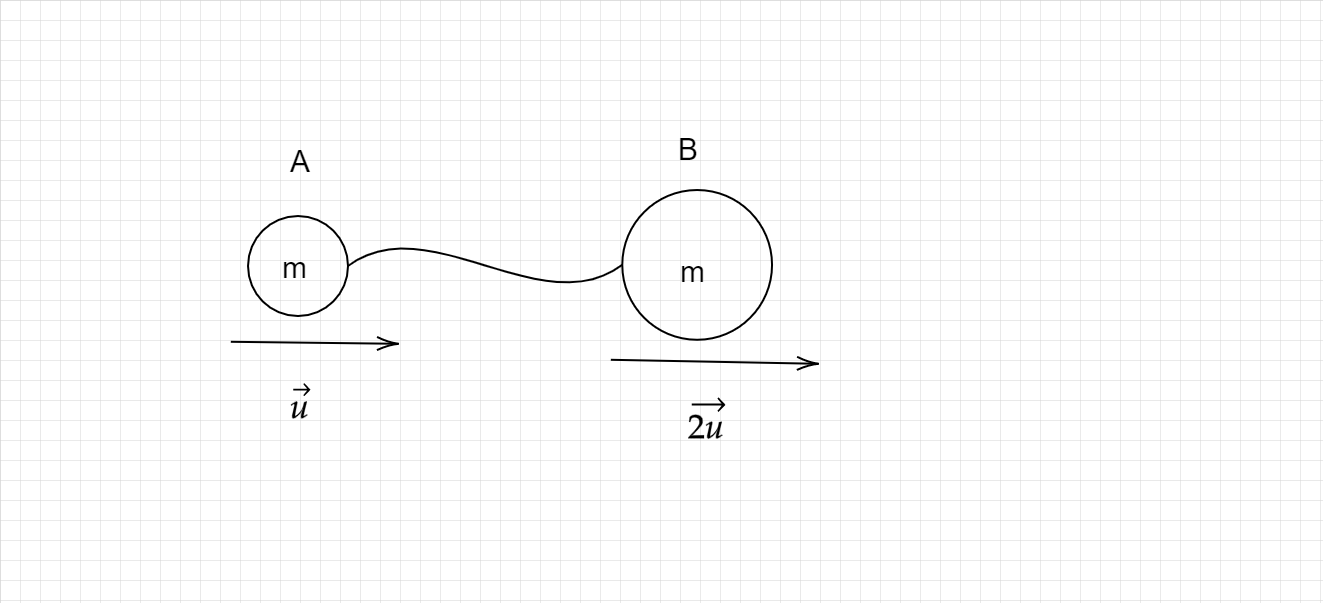
As given in the figure, the end point of the string carries the mass and Impulse value which is same in direction and value.
By rearranging the equation, the formula for the momentum:
$\vec{p}=m\vec{v}$
In the equation, where
$\vec{p}$ = the momentum $m$ = the mass of the object $\vec{v}$= the time velocity of the object
Impulse equation
Impulse = Force × (final time – initial time) Impulse = Force × $\Delta t$ $I=F\times \Delta t$
Since the impulse is a measure of how much the momentum changes we change force in the above equation with momentum. Thus, an alternative formula for impulse is
Impulse:
$\Delta p={{\vec{p}}_{final}}-{{\vec{p}}_{initial}}$
Where,
$\Delta p$ = the change in momentum ${{\vec{p}}_{final}}$= the final momentum ${{\vec{p}}_{initial}}$= the initial momentum
Using integration:

& A=\int{Idt} \\\ & \Rightarrow 2mu-mv \\\ \end{aligned}$$ Similarly, impulse equation for, $$\begin{aligned} & B=\int{Idt} \\\ & \Rightarrow mv-mu \\\ \end{aligned}$$ As we can see that both $$A$$ and $$B$$ have the same values, i.e, $$\int{Idt}$$ So, the equation then formed is, $$\begin{aligned} & A=B \\\ & \Rightarrow \int{Idt=\int{Idt}} \\\ & \Rightarrow 2mu-mv=mv-mu \\\ \end{aligned}$$ $$v=\dfrac{3}{2}u$$ Now, the impulse generated in the string, $$\begin{aligned} & \Rightarrow \int{Idt=\dfrac{3}{2}mu-mu} \\\ & \Rightarrow \dfrac{mu}{2} \\\ \end{aligned}$$ So the final answer is$$\dfrac{mu}{2}$$. Correct Option is A The formula implies that: the impulse to the change in the momentum of the object. Impulse has two different units: It is either kilogram meter per second $$\dfrac{kg-m}{s}$$ or $$N-s$$. **So, the correct answer is “Option A”.** **Note:** Car airbags and cushioned gymnasiums are examples of using the concept of impulse to reduce the force of impact. Having great racquet head speed increases the force on a tennis ball. This decreases the impact time between the ball and racquet, thereby increasing the force of impact.