Question

: What is the imaginary angular velocity of the earth at which a body placed at equator has zero weight? The radius of Earth is $6400{\text{ }}km$ and $g = 10{\text{ }}\dfrac{m}{{{s^2}}}$.
A. $\dfrac{1}{{8000}}{\text{ rad/sec}}$
B. $\dfrac{1}{8}{\text{ rad/sec}}$
C. $\dfrac{1}{{80}}{\text{ rad/sec}}$
D. $\dfrac{1}{{800}}{\text{ rad/sec}}$

Answer 1

First of all we have to find the acceleration due to gravity at the equator of the Earth. The degree of latitude at the equator is ${0^ \circ }$. From the centrifugal force that acts on the earth we will find the acceleration due to gravity. Then by substituting the values we will get the solution.

Complete step by step answer:
Consider at point P the centrifugal force acting is $mr{\omega ^2}$ where $m$ is the mass of the body, $r$ is the perpendicular distance from Y-axis and $\omega$ is the angular velocity.The weight of the body $mg$ acts downward as shown in the figure.Let $g'$ be the acceleration due to gravity at the equator.

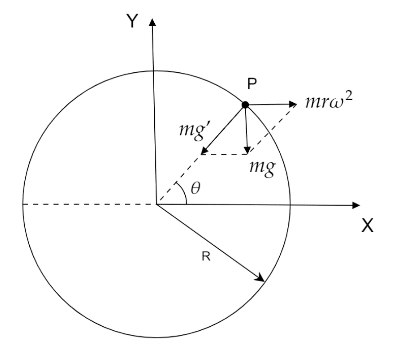
Now, from Vector law of resultant of forces we get,
$mg' = \sqrt {{{\left( {mg} \right)}^2} + \left( {mr{\omega ^2}} \right) + 2 \times mg \times mr{\omega ^2} \times \cos \left( {{{180}^ \circ } - \theta } \right)}$
Simplifying the equation and diving by $m$ we get,
$g' = \sqrt {{g^2} + {r^2}{\omega ^4} - 2gr{\omega ^2}\cos \theta }$
As, ${r^2}{\omega ^4}$ is very small hence we neglect this value.
$g' = {\left( {{g^2} - 2gr{\omega ^2}\cos \theta } \right)^{\dfrac{1}{2}}}$
$\Rightarrow g' = g{\left( {1 - \dfrac{{2r{\omega ^2}\cos \theta }}{g}} \right)^{\dfrac{1}{2}}}$
Now from binomial we get,
$g' = g - r{\omega ^2}\cos \theta$

From the given figure we get, $r = R\cos \theta$.
Substituting its value in the equation we get,
$g' = g - R{\omega ^2}{\cos ^2}\theta$
In the case of the equator, $\theta = {0^ \circ }$.
Hence, $\cos {0^ \circ } = 1$.
So, we get the acceleration due to gravity at equator as,
$g' = g - R{\omega ^2} - - - - - \left( 1 \right)$
The radius of the Earth given in the question $= 6400{\text{ }}km = 64 \times {10^5}{\text{ }}m$
$g = 10{\text{ }}\dfrac{m}{{{s^2}}}$.

Substituting the values in equation $\left( 1 \right)$ we get,
$g' = 10 - 64 \times {10^5} \times {\omega ^2}$
According to the given question, the weight of the body at the equator is $0$.
So, the mass cannot be $0$ hence, $g' = 0$.
So, we get,
$0 = 10 - 64 \times {10^5} \times {\omega ^2}$
$\Rightarrow \omega = \sqrt {\dfrac{1}{{64}} \times {{10}^{ - 4}}} \therefore \omega = \dfrac{1}{8} \times {10^{ - 2}} = \dfrac{1}{{800}}$
So, the angular velocity is $\dfrac{1}{{800}}{\text{ }}rad/\sec$.

Hence, the correct option is D.

Note: It must be noted that it was given that the weight of a body is zero. So, the weight of a body is expressed as $W = mg$. It can be zero when either the mass or acceleration due to gravity is zero. Mass can never be zero, so finally acceleration due to gravity $g = 0$. The angle used is the angle in latitude, as the equator is the ${0^ \circ }$ latitude.