Question

What is the image of $(-2,-5)$ reflected across $x=2$?

Answer 1

We are given a point and we are asked to find the coordinate of its reflection across $x=2$. We know that the line $x=2$ is a line parallel to the y – axis. Since, we have to find the coordinate of the reflection of the given point, we know that the image is formed at the same distance from the line as that of the given point from the line. So, we will first find the distance between the point $(-2,-5)$ and the line $x=2$. Then, we will add up the distance to the line $x=2$ and we will have the x – coordinate of the reflection, the y- coordinate remains the same. Hence, we will have the image of the given point across $x=2$.

Complete step by step answer:
According to the given question, we are given the coordinate of a point and we have to find the coordinate of the image as it is reflected across $x=2$.
The given point is $(-2,-5)$.
We have to find the reflection of this point across $x=2$.
We know that the distance of the image from the mirror is the same as the distance of the object from the mirror.
Applying what we know here, we will first find the distance between the point $(-2,-5)$ and the line $x=2$.
Since, y – coordinate will remain constant throughout, we won’t be using y – coordinate in our calculations.
Distance between the point and the line is, ${{x}_{2}}-{{x}_{1}}$
$=2-(-2)$
$=2+2=4$
So, from the line $x=2$, image is formed at a distance 4 units, so the x - coordinate we get is,
$x=2+4=6$
Y – coordinate remains the same, which is, $y=-5$

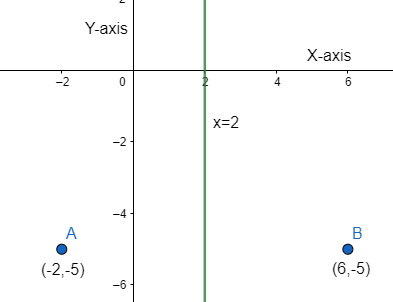
Therefore, the coordinate of the image is $(6,-5)$.

Note: The basic principle of image formation or about reflection should be recalled clearly or else the problem won’t get solved. In the above solution, the y – coordinate did not change as reflection was across $x=2$ which is a line perpendicular to the X-axis and so the image is formed horizontally.