Question

What is the ground-state term symbol for the aluminium atom in a magnetic field?

Answer 1

The term symbol in quantum mechanics is an abbreviated description of the angular momentum quantum numbers in a multi-electron system. Every energy level is not only described by its configuration but also its term symbol. The term symbol usually assumes LS coupling.

Complete Step By Step Answer:
The term symbol has a form of: $^{2S + 1}{L_J}$
Where $2S + 1$ is the spin multiplicity, L is the orbital quantum number having values S, P, D, F, G, etc. and J is the total angular momentum quantum number. The value of J ranges from ${J_{\max }} - {J_{\min }}$ (max to min) . The value of ${J_{\max }} = |L + S|$ and ${J_{\min }} = |L - S|$
The spin multiplicity or the total spin angular momentum can be given as: $S = |{M_S}| = |\sum\limits_i {{m_{s,i}}} |$ for I no. of electrons. And total orbital angular momentum quantum number L can be given as: $L = |{M_L}| = |\sum\limits_i {{m_{l,i}}} |$ for I no. of electrons. If the value of L =0,1,2,3,4, etc. it corresponds to L = S,P,D,F,G, etc, respectively.
We are given the atom Aluminum. The electronic configuration of Aluminum is given as: $Al:[Ne]3{s^2}3{p^1}$
Diagrammatically it is given as:

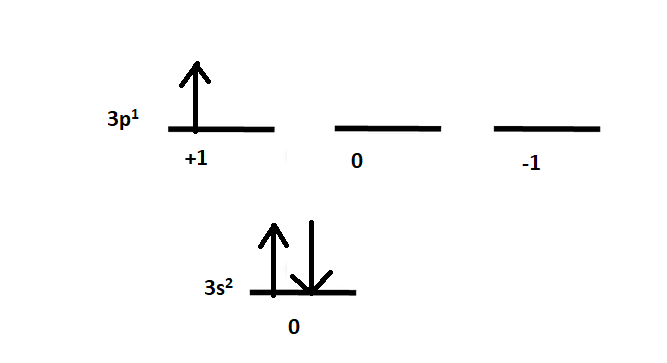
The 3s orbital has two paired electrons and 3p has one unpaired electron. Let us find the term symbols for each orbital one by one.
TERM SYMBOL FOR 3S ORBITAL:
Now, since we know the electronic configuration let us find the term symbols.
The total spin angular momentum can be given as: $S = |{M_S}| = |\sum\limits_i {{m_{s,i}}} |$
For the given configuration of electrons the value of $S = \dfrac{1}{2} - \dfrac{1}{2} = 0$
The spin multiplicity will be equal to ${S_m} = 2S + 1 = 2(0) + 1 = 1$ . Spin multiplicity = 1 indicates Singlet state.
The value of total orbital angular momentum quantum number L can be given as: $L = |{M_L}| = |\sum\limits_i {{m_{l,i}}} |$
The doubly occupied 3s orbital will have a ${m_l} = 0$ . The total angular momentum quantum number L will be: $L = |0| = 0 \to S$
The term symbol until now can be written as $^1S$
The value of J will be from ${J_{\max }} = |L + S|$ to ${J_{\min }} = |L - S|$ i.e. from ${J_{\min }} = |0 - 0| = 0$ to ${J_{\max }} = |0 - 0| = 0$ . Therefore, the value of J will be $J = 0$ . The term symbol for 3s orbital will be $^1{S_0}$
TERM SYMBOL FOR 3p ORBITAL:
Now, since we know the electronic configuration let us find the term symbols.
The total spin angular momentum can be given as: $S = |{M_S}| = |\sum\limits_i {{m_{s,i}}} |$
For the given configuration of electrons the value of $S = \dfrac{1}{2} = \dfrac{1}{2}$
The spin multiplicity will be equal to ${S_m} = 2S + 1 = 2\left( {\dfrac{1}{2}} \right) + 1 = 2$ . Spin multiplicity = 2 indicates Doublet state.
The value of total orbital angular momentum quantum number L can be given as: $L = |{M_L}| = |\sum\limits_i {{m_{l,i}}} |$
The singly occupied orbital will have a ${m_l} = + 1$ . The total angular momentum quantum number L will be: $L = | + 1| = 1 \to P$
The term symbol until now can be written as $^2P$
The value of J will be from ${J_{\max }} = |L + S|$ to ${J_{\min }} = |L - S|$ i.e. from ${J_{\min }} = |1 - \dfrac{1}{2}| = \dfrac{1}{2}$ to ${J_{\max }} = |1 + \dfrac{1}{2}| = \dfrac{3}{2}$ . Therefore, the value of J will be $J = \dfrac{1}{2},\dfrac{3}{2}$
The term symbols for 3p orbitals will thus will have two values: $^2{P_{\dfrac{1}{2}}}{,^2}{P_{\dfrac{3}{2}}}$
We are asked to find the Ground state term symbol, according to Hund’s rule:
- The term with the largest S is more stable, unless all have the same value of S.
- For terms having the same value of S and L, the subshell that has less than half filled electrons will have the smallest J and vice versa. If it has exactly half-filled electrons J will be 0.
In the given configuration the values of S and L are same, and 3p is less than half filled orbital, therefore 1/2 is more stable than 3/2. The final ground state term symbol is $^2{P_{1/2}}$ . This is the required answer.

Note:
If we are asked the ground state term symbol, the value of J will be ${J_{\min }} = |L - S|$ for less than half filled orbitals and ${J_{\max }} = |L + S|$ for more than half filled orbitals. In this case the orbital is less than half filled, hence the value of J will be ${J_{\min }} = |5 - 1| = 4$ and the ground state term symbol will be $^3{H_4}$