Question

What is the geometrical shape of an equipotential surface due to single isolated charge?

Answer 1

The direction of the electric field is always perpendicular to the equipotential surface. However, the direction of an electric field due to a point charge is always in the radial direction i.e. either radially inwards or radially outwards.

Complete solution:
When the potential is constant at any surface is called equipotential surface. The potential difference between any two equipotential surfaces always becomes Zero. In charge configuration, the equipotential at any point on the surface is normal to the electric field.

In equipotential surface at any surface which has the same electrostatic potential every point on it is called an equipotential surface. For a single isolated charge $q$, the potential is given by,
$V = \dfrac{1}{{4\pi {\varepsilon _0}}}.\dfrac{q}{r}$

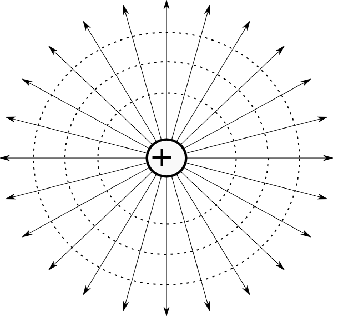
The magnitude of electric field decreases, when the centric circle and the distance between circle will increase as The electric field is,
$E = \dfrac{{kq}}{{{r^2}}}$
$\Rightarrow E = \dfrac{1}{{{r^2}}}$
Between any two points on an equipotential surface when the charge is to be moved through any path, the work done is Zero. This is because of the potential difference between two points A and B is defined as,
${V_B} - {V_A} = \dfrac{{{W_{AB}}}}{q}$
If ${V_A} = {V_B}$
Then, ${V_{AB}} = 0$
so the electric field lines should be normal to an equipotential surface.$$$$
An equipotential surface is obtained, when all the particles at same potential in the electric field are joined.
Properties of equipotential surface:
In equipotential surface, potential difference between at any two points is Zero ${V_A} - {V_B} = 0$.
The work is not done by electric force in moving a charge on an equipotential surface. In an equipotential surface due to a single isolated charge, the direction of $\vec E$ is always perpendicular.

Note: In equipotential surface, the field lines are always perpendicular. The shape of the equipotential surface is cylindrical and spherical. In String electric fields regain equipotential surface closely spaced. There is no work required to move a test charge in an equipotential surface. Two equipotentials can never be intersect.