Question

What is the formula for converting polar coordinates to rectangular coordinates?

Answer 1

When each point on a plane of a two-dimensional coordinate system is decided by a distance from a reference point and an angle is taken from a reference direction, it is known as the polar coordinate system. Rectangular coordinate system is the normal Cartesian coordinate system with coordinates x and y, denoted as $\left( x,y \right)$ . We have to derive the formula using the trigonometric functions.

Complete step-by-step answer:
Let us first see what polar coordinate systems are. When each point on a plane of a two-dimensional coordinate system is decided by a distance from a reference point and an angle is taken from a reference direction, it is known as the polar coordinate system. In the polar coordinate system, we will call the origin as a pole. Here, pole will be the reference point and the polar axis will be the line segment ray from the pole in the reference direction. Let us understand more from the figure shown below.

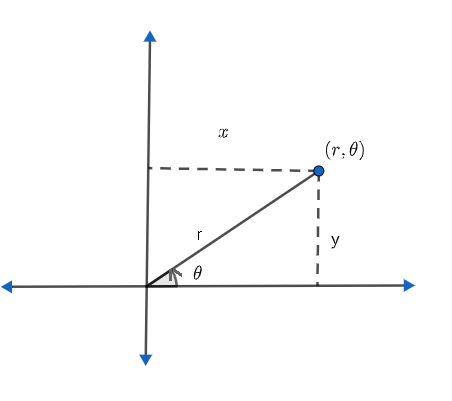
We can see that polar coordinates are $\left( r,\theta \right)$ .
Now, let us see what rectangular coordinates are. Rectangular coordinate system is the normal Cartesian coordinate system with coordinated x and y, denoted as $\left( x,y \right)$ .
Now, to convert polar coordinates to rectangular coordinates, we have to consider the below figure.

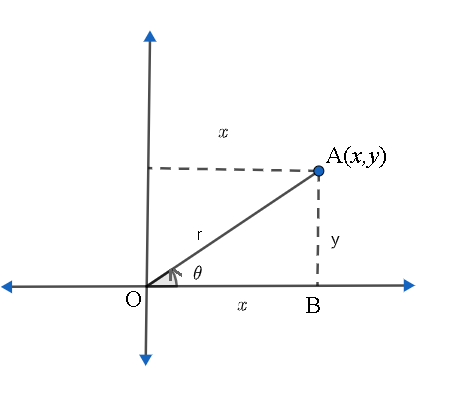
Let us say that there is a point A with coordinates $\left( x,y \right)$ . The distance from the origin to the point A is given as r. The line joining the origin to the point A makes an angle $\theta$ with the positive x-axis. Now, we have to find the value of x and y. We know that triangle AOB is a right-angled triangle. From the figure, we can see that
$\cos \theta =\dfrac{\text{Adjacent side}}{\text{Hypotenuse}}=\dfrac{x}{r}$
From the above equation, we have to take the denominator of the RHS to the LHS.
$\Rightarrow x=r\cos \theta$
Similarly, from the figure, we can see that
$\sin \theta =\dfrac{\text{Opposite side}}{\text{Hypotenuse}}=\dfrac{y}{r}$
Let us take r to the LHS.
$\Rightarrow y=r\sin \theta$
Hence, the formulas for converting polar coordinates to rectangular coordinates are
$x=r\cos \theta$ and $y=r\sin \theta$ .

Note: In the solution, we have considered a two-dimensional system. For a three-dimensional system, we will have to consider one more coordinate, that is, z for both the rectangular and polar coordinate system. This coordinate will be equal.