Question

What is the force required for uniform circular motion?

Answer 1

First of all we have to understand what uniform circular motion is. Then with the help of a diagram, using vectors, we will understand about the acceleration of a uniform circular motion. Then from Newton’s Second Law we know that the multiplication of the mass of any body with respect to acceleration is known as force.

Complete step by step answer:
The circular motion where the speed of the particle does not change with time is known as uniform circular motion. So, the speed $v$ is constant and angular speed $\omega$ is constant.
So, we get the tangential acceleration and angular acceleration as $0$but the particle is still accelerating.
So, the acceleration thus produced is called centripetal acceleration and the force is known as centripetal force.
Consider a particle moving on a circular path of radius $r$ and centre O, with a uniform speed $v$, as shown in figure. Let the particle be at point P at time $t$, and at Q at time $t + \Delta t$. Let $\overrightarrow {{v_1}}$ and $\overrightarrow {{v_2}}$ be the velocity vectors at P and Q directed along the tangents at P and Q respectively.
To find the change in velocity, take an external point A. Draw vectors $\overrightarrow {{\text{AB}}}$ and $\overrightarrow {{\text{AC}}}$ such that $\overrightarrow {{\text{AB}}} = \overrightarrow {{v_1}}$ and $\overrightarrow {{\text{AC}}} = \overrightarrow {{v_2}}$.

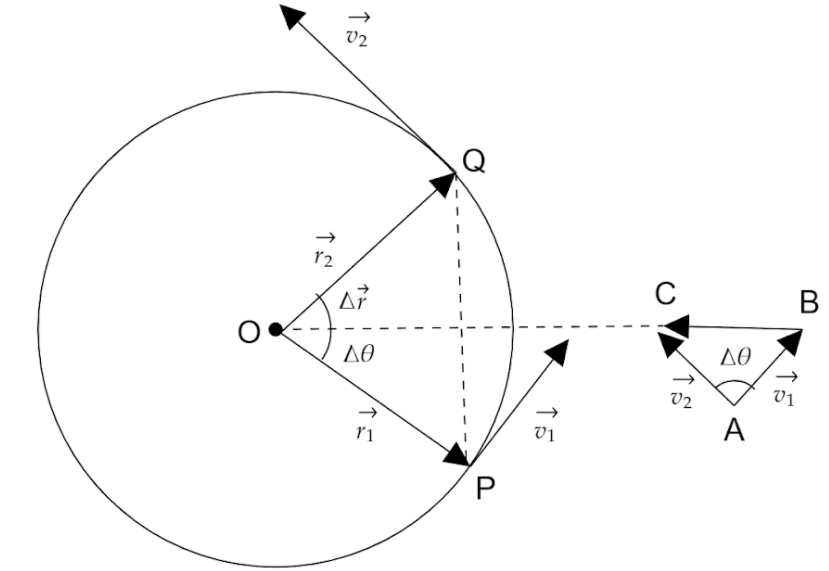
Draw the vector $\overrightarrow {{\text{BC}}}$ close to the triangle.
According to the triangle law of vector addition,
$\overrightarrow {{\text{AB}}}$ $+$ $\overrightarrow {{\text{BC}}}$ $=$ $\overrightarrow {{\text{AC}}}$
Changing sides we get,
$\overrightarrow {{\text{BC}}} = \overrightarrow {{\text{AC}}} - \overrightarrow {{\text{AB}}}$
$\overrightarrow {{\text{BC}}} = \overrightarrow {{v_2}} - \overrightarrow {{v_1}} = \Delta \overrightarrow v$
This is the change in velocity during this time interval $\Delta t$.
By definition, the average acceleration is given by,
$\overrightarrow {\overline a } = \dfrac{{\Delta \overrightarrow v }}{{\Delta t}}$ where $\overrightarrow {\overline a }$ is along $\Delta \overrightarrow v$.
Since the path is circular, $\overrightarrow {{v_1}}$ is perpendicular to $\overrightarrow {{r_1}}$, and so is $\overrightarrow {{v_2}}$ to $\overrightarrow {{r_2}}$. Therefore $\Delta \overrightarrow v$ too is perpendicular to $\Delta \overrightarrow r$.As $\Delta t \to 0$ the average acceleration becomes the instantaneous acceleration and $\Delta \theta$ approaches to $0$.
In this limit, $\overrightarrow {{\text{AB}}}$ $=$ $\overrightarrow {{\text{AC}}}$, so $\angle {\text{ABC = }}\angle ACB = {90^ \circ }$. Thus, $\Delta \overrightarrow v$ and hence $\overrightarrow a$ is perpendicular to velocity vector $\overrightarrow {{v_1}}$. But since $\overrightarrow {{v_1}}$ is directed along the tangent at point P, so acceleration $\overrightarrow a$ acts along the radius towards the centre of the circle , that is why the acceleration is called centripetal acceleration.
Thus, from Newton’s Second Law $\overrightarrow F = m\overrightarrow a$, hence this force which is dependent on centripetal acceleration is known as centripetal force.

Note: It must be kept in mind that tangential force exists in circular motion only when the speed changes in time. When the speed does not change in case of uniform circular motion the tangential force is $0$. While in circularly rotating bodies, there exists non-zero centripetal force which changes the direction of motion.