Question

What is the flux over a curved surface of the hemisphere?

Answer 1

The rate of flow of electric field lines through a given area is known as electric flux $\left( {{\phi _E}} \right)$ .$S.I$ Unit for electric flux is $\left( {\dfrac{{N{m^2}}}{C}} \right)$ . Area vector$\overrightarrow {(A)}$ is a vector whose magnitude is equal to the area and direction is perpendicular and away from the surface.

Complete step by step answer:
The electric flux over a curved surface area of the hemisphere can be represented as shown in the figure below, let $R$be the radius of the hemisphere.

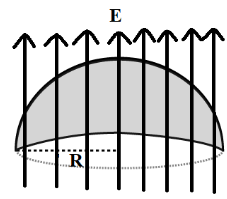
The electric flux$\left( {{\phi _E}} \right)$ is given by the equation,
${\phi _E} = EA\cos \theta$.
Where $\theta$ is the angle between electric field $\left( E \right)$ and area vector $\left( A \right)$.
${\phi _E} = EA\cos 180$.
The angle between the electric field $\left( E \right)$ and the area vector $\left( A \right)$is ${180^0}$.
${\phi _E} = - EA$.......................$\left( {\because \cos 180 = - 1} \right)$
We know that, the area of circle is $\pi {r^2}$,
$\therefore {\phi _E} = - E\pi {R^2}$

Hence, the flux over a curved surface of the hemisphere is $- E\pi {R^2}$.

Note: We need to consider the area of the circle not the area of the hemisphere because the electric field lines pass through the base of the hemisphere and the base of the hemisphere is a circle. Negative sign indicates that the direction of electric field lines and area vectors is opposite.