Question
Question: What is the final image position from third lens? \(({f_1} = 10cm,{f_2} = - 10cm,{f_3} = 30cm)\) !...
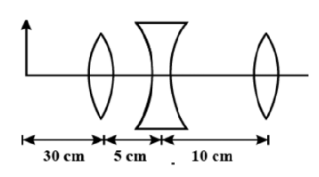
What is the final image position from third lens? (f1=10cm,f2=−10cm,f3=30cm)
A. 15cm
B. infinity
C. 45cm
D. 30cm
Solution
Lens formula derived from let F be the principal focus and f be the focal length. An object AB is held perpendicular to the principal axis at a distance beyond the focal length of the lens. To give the values of focal length of the lens, we find the final image position from the third lens. Also, we use the lens formula.
Complete step-by-step answer:
It is given that the Focal length of first lens =10cm
Focal length of second lens =−10cm
Focal length of first lens =30cm
Object distance from first lens =30cm
Now, calculate the image distance for first lens
Using lens formula, v1+f1+u1
v1=f1+u1
Put the value into the formula
⇒ v1=101+−301
Taking LCM we get,
⇒ v1=−30−3+1
On subtracting the numerator term and we get,
⇒ v1=−30−2
On cancelling term we get,
⇒ v1=151
Now, we get v=15cm
Also, calculate the image distance for second lens
Using lens formula
v1+f1+u1
Here, u=5−15=−10cm
Put the value into the formula
⇒ v1=−101+101
On adding we get,
⇒ v1=01
Therefore, v=∞
Now, we calculate the image distance for third lens
Using lens formula
⇒ v1+f1+u1
Put the value into the formula
⇒ v1=301+∞1
Here, ∞1=0
⇒ v1=301
Therefore, v=30cm
The final image is formed to 30cm right of the third lens.
So, the correct answer is option (D).
Note: The focal distance of a lens is decided when the lens is concentrated at infinity. Lens focal length tells us the angle of view- what proportion of the scene is getting to be captured and thus the magnification- how large individual elements are getting to be. The longer the focal length, the narrower the angle of view and thus the upper the magnification.
It is not measurement of the particular length of a lens, but a calculation of an optical distance from the purpose where light rays converge to form the purpose where light rays converge to make a sharp image of an object to the digital sensor or 35mm film at the focal plane within the camera. The focal length of a lens is set when the lens is concentrated at infinity.
