Question
Question: What is the expression of mutual inductance for shown concentric co – planar circular and regular he...
What is the expression of mutual inductance for shown concentric co – planar circular and regular hexagon (a>>r) ?
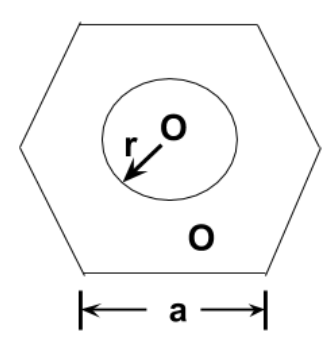
Solution
Construct an equilateral triangle of height d inside the hexagon. Find the magnetic field for one side of the hexagon and then for all of its sides. Use the Biot – Savart’s Law for this which can be expressed as:
dB=4πμ0r2Idl.sinθ
where, I is the amount of current in the loop and r is the radius of that loop.
Complete step by step solution:
As this question is to be solved by using the Biot – Savart’s Law so, we should know what it is? The equation which gives the magnetic field produced due to the current carrying segment is known as Biot – Savart’s Law. The formula of Biot – Savart’s Law is:
dB=4πμ0r2Idl.sinθ
where, I is the amount of current in the loop and r is the radius of that loop.
Now, we have to make some construction in the figure given in the question. Therefore,
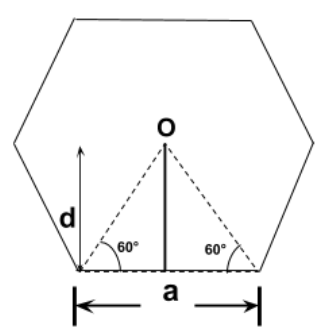
Let the current flowing in the hexagon be I.
Now, by using the Biot – Savart’s Law, the magnetic field at centre O due to one side of hexagon is:
B1=2πdμ0Icos60∘ ⇒B1=4π23aμ0I
There are 6 sides in the hexagon, therefore, to calculate the magnetic field at centre O due to all of its six sides we have to multiply B1 with 6. So, -
⇒B=6B1 ⇒B=64π23aμ0I ∴B=πa3μ0I
Hence, the flux through the circular loop can be calculated as –
ϕ=B×πr2
Putting the value of magnetic field in the above equation of flux –
ϕ=πa3μ0I×πr2 ⇒ϕ=a3μ0Ir2
Now, we know the relation between the mutual induction and flux which can be expressed as:
ϕ=MI
where, M is the mutual induction and I is the current flowing in the loop.
So, the above relation can also be written as –
⇒M=Iϕ
Putting the value of flux in the above expression of mutual induction, we get –
⇒M=Ia3μ0Ir2 ∴M=a3μ0r2
Hence, the required expression of mutual induction is a3μ0r2.
Note: It is not necessary to find the magnetic field at the centre due to each side of the hexagon, you can find it from one side and multiply it with six to get the overall magnetic field of the loop.
