Question

What is the equivalent resistance of the circuit?

A. $20$ohms
B. $10$ohms
C. $5$ohms
D. $2\text{ }$ohms

Answer 1

The total resistances of resistors series is the sum of their individual resistance and the total resistance of resistors in parallel are is the sum of the reciprocal of their resistance.

Formula used:
For two resistors ${{R}_{1}}$ and ${{R}_{2}}$ is series, total resistance R is given by
$R={{R}_{1}}+{{R}_{2}}$
For two resistors ${{R}_{1}}$ and ${{R}_{2}}$ is parallel, total resistance R is given by
$\frac{1}{R}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}$

Complete step by step solution:

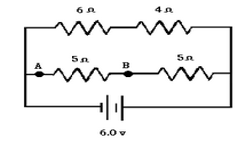
The given circuit is a parallel circuit containing two branches. In one branch, there is a $6\text{ }\Omega$ and a $\text{4 }\Omega$ resistor, and in the other branch there are two $\text{5 }\Omega$-resistors.
In the circuit, the $6\text{ }\Omega$-resistor is in series with the $\text{4 }\Omega$-resistor and the two $\text{5 }\Omega$ resistors are in series with each other.
So the equivalent resistance in one branch (containing $6\text{ }\Omega$ and $\text{4 }\Omega$ resistor) is:
${{R}_{1}}=4\text{ }\Omega +\text{6 }\Omega =10\text{ }\Omega$
The equivalent resistance in the other branch (containing two $\text{5 }\Omega$-resistors) is
${{R}_{2}}=5\text{ }\Omega +5\text{ }\Omega =10\text{ }\Omega$
Therefore, ${{R}_{1}}$ and ${{R}_{2}}$ is parallel, so, equivalent resistance R of the circuit is given by

& \frac{1}{R}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}} \\\ & \frac{1}{R}=\frac{1}{10\text{ }\Omega }+\frac{1}{10\text{ }\Omega } \\\ & \frac{1}{R}=\frac{2}{10\text{ }\Omega } \\\ & R=5\text{ }\Omega \\\ \end{aligned}$$ **So, option C is the correct answer.** **Additional information:** It is convenient to connect electrical components in parallel, as when disconnecting one component the other components are not switched off. **Note:** In a parallel circuit, the voltage across each component is the same, but the current through each branch is different. The total current is equal to the sum of currents in individual branches. The equivalent resistance of the circuit is less than the equivalent resistance in each branch. The total resistance will decrease with addition of more components. In a series connection, the components are connected in one single branch, back to back, and the current through each component is the same, whereas the voltage across each component is different.