Question
Question: What is the equivalent resistance between points \(A\) and \(B\)? 
Solution
The cumulative resistance of a series circuit is precisely the sum of the resistances of the circuit's components. Since current will pass through several pathways in a parallel circuit, the total overall resistance is lower than the resistance of any single part.
Formula used:
The formula to calculate resistance in series combination is:
R=R1+R2+R3+....+Rn
And the formula to calculate the resistance in parallel combination is:
R1=R11+R21+R31+...+Rn1
Complete step by step answer:
To calculate the total resistance , we will divide the circuits into different parts. Firstly, we combine R3 and R4, these combinations are in series.
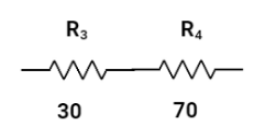
Hence, we sum up the values.
70+30=100Ω
Now, this 100Ω is in parallel combination with R2.Hence,
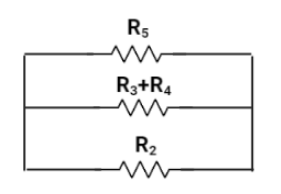
R1=1001+1001 ⇒R1=1001+1 ⇒R1=1002 ⇒R=50Ω
Now, The resistance 50Ω is in parallel with R5. Hence, we will get,
R1=501+501 ⇒R1=502 ⇒R=25Ω
Now, this 25Ω resistance is in series with R1.
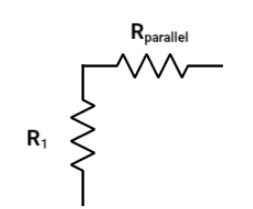
Hence we get,
R=50+25 ∴R=75Ω
Hence, the equivalent resistance between point A and B is 75Ω.
Note: Resistor Combination or mixed resistor circuits are resistor circuits that incorporate series and parallel resistor networks together. The procedure for measuring the equivalent resistance of the circuit is the same as for any other series or parallel circuit.
