Question
Question: What is the equivalent capacitance of the system of capacitors between A and B as shown in the figur...
What is the equivalent capacitance of the system of capacitors between A and B as shown in the figure.
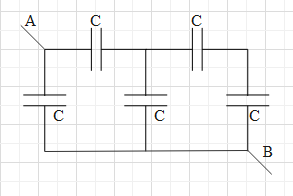
A. 67C
B. 1.6C
C. C
D. none
Solution
The given circuit forms a wheatstone bridge. Therefore, check whether the given wheat stone bridge is balanced or not, i.e. whether the four capacitances satisfy the relation C2C1=C4C3. Then, use the formula for equivalent capacitance between two capacitances when they are series i.e. Ceq1=C11+C21 and when they are in parallel i.e. Ceq=C1+C2.
Formula used:
C2C1=C4C3
Ceq=C1+C2
Ceq1=C11+C21
Complete step by step answer:
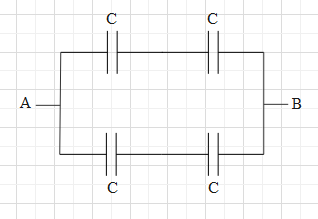
Let us first redraw the given figure as given below.
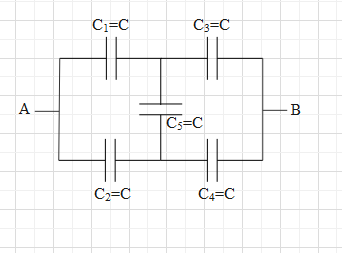
Now, from this figure we can see that the given combination makes up a wheat-stone bridge. When the fours capacitors given in the wheatstone bridge satisfy the relation C2C1=C4C3, the potential difference across the fifth capacitor (C5) is zero. And we say that the circuit is balanced.
Therefore, let us check whether the given wheat stone bridge is balanced. Here, all the capacitors have the same capacitors. That is, C1=C2=C3=C4=C.
Therefore,
C2C1=CC=1 …. (i)
And
C4C3=CC=1 ….. (ii)
From (i) and (ii), we get that C2C1=1=C4C3
⇒C2C1=C4C3.
This means that the wheatstone bridge is balanced and the potential difference across the capacitor C5 is 0.
Since the potential difference across the capacitor C5 is zero, we can remove the capacitor and short the circuit at that position.
After this, the circuit will look as shown below.
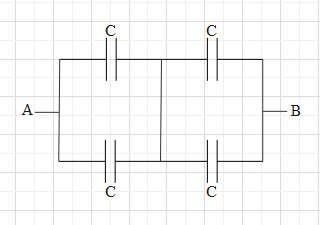
Now, the capacitors C1 and C2 are parallel connections. When two capacitors are in parallel connection, the equivalent capacitance is equal to the sum of the individual capacitances.
This means that,
Ceq=C1+C2
⇒Ceq=C+C=2C.
Similarly, the capacitors C3 and C4 are also in parallel connection. Hence, the equivalent capacitance of these two is Ceq=C3+C4=C+C=2C.
Now, the given circuit will look as shown below.
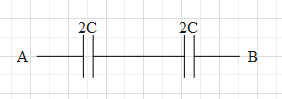
As we can see, the capacitances are in series. We two capacitors are in series connection, the reciprocal of the equivalent capacitance is equal to the sum of the reciprocals of the individual capacitances.
The means that equivalent capacitance of the given combination is Ceq1=2C1+2C1.
⇒Ceq1=2C2=C1
⇒Ceq=C.
Therefore, the equivalent capacitance of the given system of capacitors is C.
Hence, the correct option is C.
Note:
After the wheat stone bridge is balanced, instead of shorting the capacitor C5, we can leave the circuit open as shown.
Now, C1 and C3 are series. Therefore, the reciprocal of the equivalent capacitance of these two capacitors will be Ceq1=C11+C31=C1+C1=C2.
⇒Ceq=2C.
Similarly, the equivalent capacitance of C2 and C4 will be 2C.
Therefore, the circuit can be simplified as shown.
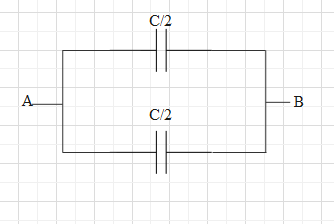
Now, the two capacitances are in parallel. Therefore, the equivalent capacitance will be Ceq=2C+2C=C.
