Question
Question: What is the equivalent angle of one radian? (A) \({53.3^ \circ }\) (B) \({54.3^ \circ }\) (C) ...
What is the equivalent angle of one radian?
(A) 53.3∘
(B) 54.3∘
(C) 57.3∘
(D) 55.3∘
Solution
In order to calculate the angle of any object we have two methods. They are degrees and radians. Radian is one to express an angle. Radian is denoted by the symbol rad which is the S.I. unit for calculating angle of a circle.
Complete step by step solution:
The calculation of radian of a mean angle circle can be explained as the proportion of the distance of the curve of a mean angle circle specific by the angle to that of the distance of the radius of the circle. In order to fully grasp the concept of radian let’s assume a circle of radius of r , mean angle θ and the specific curve distance l. According to the mean angle circle radian is expressed as;
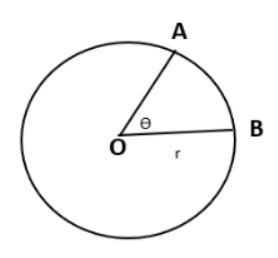
θ=rl
We can constitute θ as one radian, when l=r ;
θ=rr
θ=1
For the calculation of one radian in degree;
Let us consider a semicircle where the mean angle is 180∘ . the number of radians that are required to replace the mean angle of the semicircle is more or less equal to 3.14 π. Where π can be explained as the proportion of the diameter of the circle is divided to the circumference of the circle.
Since π is a radian equal to 180∘ we can say that;
1 radian =π180∘=57.3∘
Therefore, one radian is equivalent to 57.3∘
Hence, the option (C), 57.3∘ is the correct answer.
Note: In order to convert to degree to radian the formula is multiply the angle by 180∘π and in order to convert to radian to degree the formula is multiply the angle by π180∘ . While solving this problem make sure to draw the diagram of the mean circle and mark the necessary details, it will be helpful in determining the angle.
