Question
Question: What is the equation of the parabola with focus \(\left( 0,\dfrac{1}{8} \right)\) and vertex at the ...
What is the equation of the parabola with focus (0,81) and vertex at the origin?
Solution
For the given question we must know the equation of parabola for all the cases and must know the concept and about every variable that is used in the equation in order to substitute the values and understand its graph in order to answer the questions.
Complete step by step solution:
Parabola is a curve where every point is at equal distance from the focus and the directrix which is a fixed straight line. The axis of symmetry of parabola passes through the focus and at right angles to the directrix. The vertex of parabola is where the graph makes the sharpest turn and it is halfway between the directrix and the focus.
We are given the focus as (0,81) and the vertex as the origin i.e. (0,0).
To find the line of symmetry we find the common component. We see that the x-coordinate of both origin and vertex is 0, so it is clear that it is a vertical parabola.
The general equation of a vertical parabola is:
(x−h)2=4a(y−k)
To calculate ‘a’ we simply subtract the y-coordinates since it is a vertical parabola, so
a=81−0=81
Now, the parabola passes through the origin so we put the values of ‘h’ and ‘k’ as 0.
Putting these values, we get:
(x−0)2=4×81×(y−0)
After simplifying, we get the equation of parabola as:
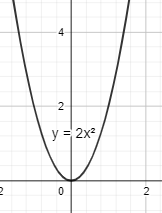
x2=21×y
⟹2x2=y
Hence, the equation of parabola is obtained.
Note: Parabola has various properties and we must know how the vertex and focus and directrix are present in the parabola as all the questions frames from this section would be majorly based on these three terms or will definitely make use of these.
