Question
Question: What is the equation of the parabola which has a vertex at the origin with a focus at \[\left( 5,0 \...
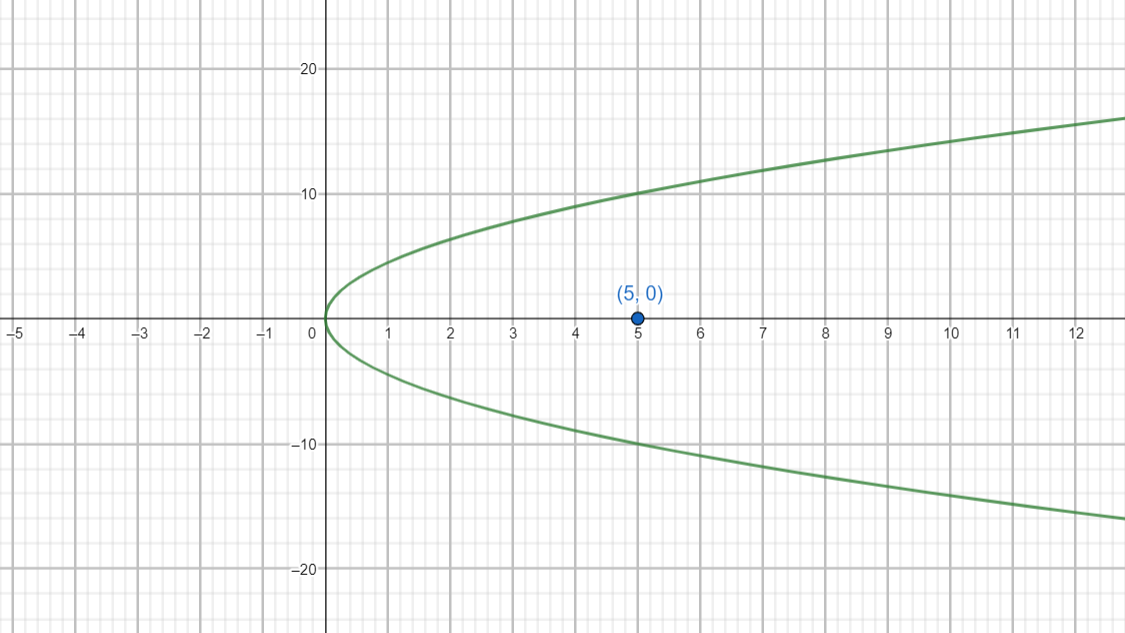
What is the equation of the parabola which has a vertex at the origin with a focus at (5,0)?
Solution
The standard parabola equation having its axis of symmetry parallel x axis and having vertex at (h,k) is (y−k)2=4a(x−h), focus is at(a+h,0).given vertex (0,0)and focus (5,0).we can see the coordinates of the y are zero, so both focus and vertex lie on the x axis.
Focus is at the right of the vertex, so the parabola opens right.
Complete step-by-step answer:
From the question we were given a vertex at the origin and focus at (5,0).
Now we have to find the equation of parabola.
From the given information, the parabola opens right because focus is at the right of the vertex.
from the standard parabola equation having its axis of symmetry parallel toxaxis and having vertex at (h,k) is (y−k)2=4a(x−h).
⇒(y−k)2=4a(x−h)…….………(1)
From the question we were given vertex at (0,0)
So,
⇒(h,k)=(0,0)
substitute (h,k)=(0,0) in equation (1), now we will get
⇒(y−0)2=4a(x−0)
On simplification we will get,
⇒y2=4ax…………….(2)
We were given focus at (5,0)
We know focus is at (a+h,0)
so,(a+h,0)=(5,0)
⇒(a+0,0)=(5,0)
⇒(a,0)=(5,0)
So, a=5.
Now put a=5 in equation (2)
⇒y2=4ax
⇒y2=4×5×x
Om multiplication of 4 and 5 we get 20
So, the equation becomes
⇒y2=20×x y2=20x
⇒y2=20x
The parabola equation having vertex at the origin and focus at (5,0) is y2=20x.
Let us try to represent y2=20x on the graph.
Note: students may have a misconception that parabola equation can also be (x−h)2=4a(y−k). But this is the equation when the axis of symmetry is parallel to y. Here we are given a symmetry parallelxaxis so we have to use (y−k)2=4a(x−h). Students should be accurate in calculations.
