Question

What is the equation of the parabola that has a vertex at $\left( 2,-9 \right)$ and passes through the point $\left( 12,-4 \right)$ ?

Answer 1

To find the equation of the parabola that has a vertex at $\left( 2,-9 \right)$ and passes through point $\left( 12,-4 \right)$ , we have to consider the vertex form of the parabola which is given by $y=a{{\left( x-h \right)}^{2}}+k$ , where “a” is the distance from the origin to the focus and $\left( h,k \right)$ is the vertex. We have to substitute the given vertex in the above formula. Then, we have to find the value of a from the given point by substituting the point in the vertex form. Then, we have to solve for a and substitute this value of a in the vertex form which we obtained after substituting the vertex.

Complete step-by-step solution:
We have to find the equation of the parabola that has a vertex at $\left( 2,-9 \right)$ and passes through point $\left( 12,-4 \right)$ . We know that the equation of a parabola with vertex $\left( h,k \right)$ is given by
$y=a{{\left( x-h \right)}^{2}}+k$
where “a” is the distance from the origin to the focus.
We are given that the parabola has vertex $\left( 2,-9 \right)$ . Here, we can see that $h=2$ and $k=-9$ . Hence, we can write the formula of parabola as
$y=a{{\left( x-2 \right)}^{2}}-9...\left( i \right)$
Now, we have to find a. We are given that the parabola passes through the point $\left( 12,-4 \right)$ . Let us substitute $x=12$ and $y=-4$ in the above equation.
$\Rightarrow -4=a{{\left( 12-2 \right)}^{2}}-9$
We have to solve for “a”. Let us first simplify the terms inside the bracket.
$\begin{aligned} & \Rightarrow -4=a{{\left( 10 \right)}^{2}}-9 \\\ & \Rightarrow -4=100a-9 \\\ \end{aligned}$
Let us take -9 from RHS to the LHS.
$\begin{aligned} & \Rightarrow -4+9=100a \\\ & \Rightarrow 5=100a \\\ & \Rightarrow 100a=5 \\\ \end{aligned}$
We can now find a by taking 100 to the RHS.
$\Rightarrow a=\dfrac{5}{100}=\dfrac{1}{20}$
Now, we have to substitute this value of a in the equation (i).
$y=\dfrac{1}{20}{{\left( x-2 \right)}^{2}}-9$
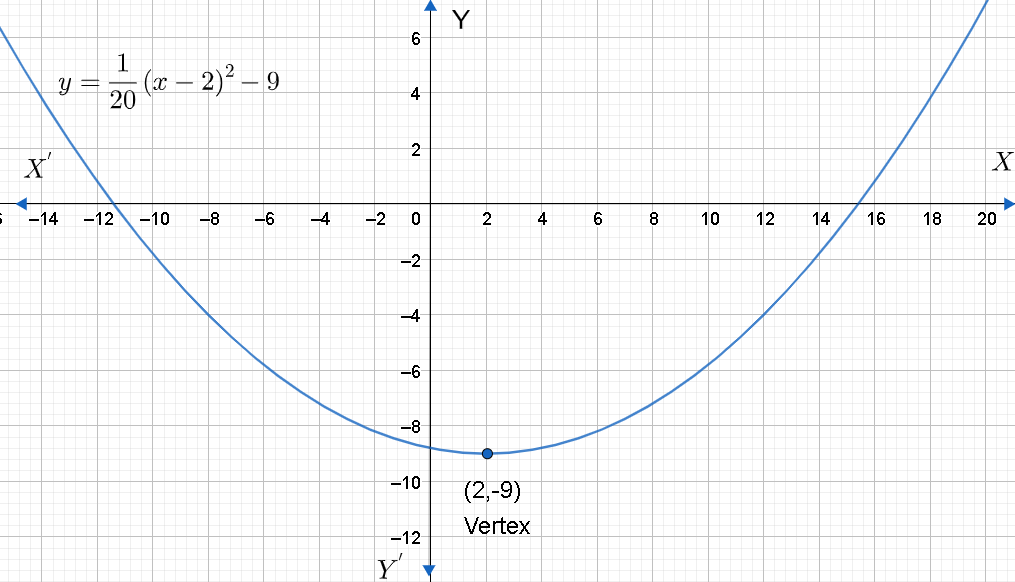
Thus, the equation of the parabola that has a vertex at $\left( 2,-9 \right)$ and passes through point $\left( 12,-4 \right)$ is $y=\dfrac{1}{20}{{\left( x-2 \right)}^{2}}-9$.

Note: Students must know the standard and vertex form of a parabola. Standard form is given by $y=a{{x}^{2}}+bx+c$ . We did not use this formula in this question because the standard formula does not involve vertex. Let us draw this parabola. We can see that a is positive. Therefore, the parabola opens upwards. If a is negative, then the parabola opens downwards.