Question

What is the equation of the line that has a slope of $m = \dfrac{2}{3}$ and goes through$(0,5)$ ?

Answer 1

Use the general equation of a straight line and substitute values of slope and the given coordinates to figure out the equation of this straight line.
Formula Used: $y = mx + c$

Complete step-by-step solution:
The information given to us in the question tells us that there exists a line in the Cartesian plane which passes through coordinates $(0,5)$, where 0 lies on the $X - axis$ and $5$ lies on the $Y - axis$. The term $m$ here denotes the slope of the straight line that we are talking about here. Slope of a straight line in coordinate geometry, also referred to as the gradient of a line, is defined as the measure of steepness of the line with respect to the $X - axis$ and the $Y - axis$. Slope of a line can have negative as well as positive value, depending on the degree and sharpness of change between both the axes for a line. The given value of $m$ in this question is $\dfrac{2}{3}$. We will use this information to write the equation of a line which satisfies the criteria mentioned in the question.
The simplest way to write represent a straight line in Cartesian plane is to write it in the form of
$y = mx + c$,
Where $c$ is the intercept of the line on $Y - axis$, that is, it is the point on $Y - axis$ where the straight line cuts the axis, and $m$ is the slope of the straight line.
Hence, putting the value of $m$ from the question in the equation for a straight line, we get, $y = \dfrac{2}{3}x + c$
While this equation has a value of $m$ and is written in terms of $x$ and $y$, it is still incomplete. To complete this equation, we need to find a fixed value of intercept $c$. To find out the value of $c$, we will substitute the values of $0$ in place of $x$ and $5$ in place of $y$. We do this because if the given straight line passes through $(0,5)$, then these values will satisfy the equation for this straight line. Hence, substituting the values we get,
$5 = \dfrac{2}{3} \times (0) + c$
On simplifying we get,
$c = 5$.
Hence the value of the$Y - axis$ intercept is $5$. Now, substituting the values of$c$ and $m$ in the general equation we get, $$$$
$y = \dfrac{2}{3}x + 5$
To represent this equation in proper form, we multiply the entire equation by $3$ to get rid of the fraction, and we get,
$3y = 2x + 15$
And rearranging this equation we get,
$2x - 3y + 15 = 0$
Hence the equation of a line passing through $(0,5)$ having slope $\dfrac{2}{3}$ is $2x - 3y + 15 = 0$.

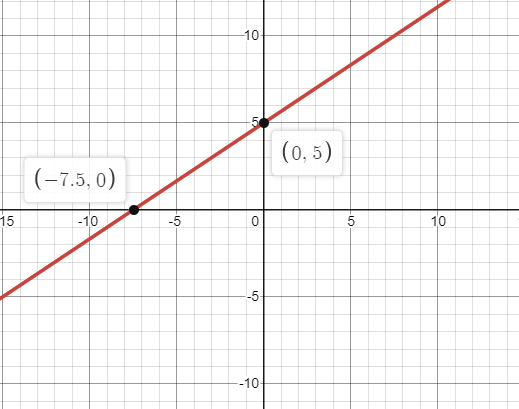
Here the graph represents our straight line.

Note: Make sure that there are no fractions present in the equation. In case there are multiple fraction coefficients in the equation, multiply the entire equation with the LCM (Least Common Multiple) of all the denominators present in the equation to arrive at the proper form of the equation.