Question

What is the equation of the line normal to $f\left( x \right) = {x^2} - x + 2$at $x = 1$

Answer 1

First, find the equation of the line tangent to the function at the point; then we have to find their equation of the tangent line to the function at the point. Then we find the equation of the line finds the line posses through the point but it has a perpendicular slope.

Complete answer:
We have to find the equation of the tangent line to the function at the point.
Then find the equation of the line.
Find the line that passes through the point. But has a perpendicular slope.
The given equation is$f\left( x \right) = {x^2} - x + 2$
Here given the value $x = 1$
Substitute the value in the given equation
$f\left( 1 \right) = {1^2} - 1 + 2$ $= 2$
Solve the equation we get,
$= 2$
Differentiate the equation with respect to$x$what we get,
$f'\left( x \right) = 2x - 1$
Substitute the given $x$value
$f'\left( 1 \right) = 2\left( 1 \right) - 1$
$f'\left( 1 \right) = 1$
We have the point and the slope of the line tangent to the $f\left( x \right)$at$x = 1$
From the given equation we get
Tangent line is
$y = 1\left( {x - 1} \right) + 2$
Take $x$ as common and substitute $x = 1$
Simplify the equation, we get
$y = x - 1 + 2$
$y = x + 1$
Therefore simplified tangent line is,
$y = x + 1$
Since the slope is one, the slope of the normal line is$\dfrac{{ - 1}}{1} = - 1$
We know that the slope of the normal line to the graph $f\left( x \right)$is$\dfrac{{ - 1}}{{f'\left( x \right)}}$
We have to find the normal line.
Therefore normal line is
$y = - 1\left( {x - 1} \right) + 2$
Simplify the equation and have
$y = - x + 1 + 2$
$y = - x + 3$
Hence the equation of the line normal is $y = - x + 3$

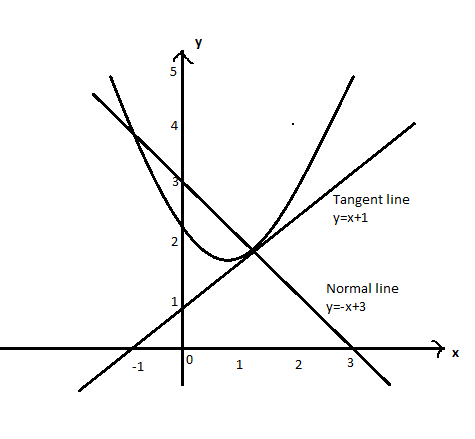
Note:
The normal line to a curve at a particular point is the line through that point and perpendicular to the tangent. A person might remember from analytic geometry that the slope of any line perpendicular to a line with slope m is the negative reciprocal$- 1/m$