Question

What is the equation of parabola with a vertex at $\left( {2,3} \right)$ and focus at $\left( {6,3} \right)$ ?

Answer 1

Hint : The given problem tests us on the concepts of coordinate geometry as well as conic sections. The problem requires us to find the equation of the parabola whose coordinates of vertex and focus are provided to us in the question itself. We first have to analyze the problem by drawing a figure for the situation and then plan our sequence of actions. Such problems put our knowledge of all the fields of mathematics such as algebra, calculus, conic sections and analytical geometry to test.

Complete step by step solution:

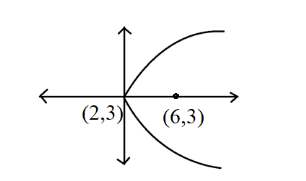
So, in the given problem, we are required to find the equation of the parabola with a vertex at $\left( {2,3} \right)$ and focus at $\left( {6,3} \right)$ .
Now, we know that the vertex and focus of a parabola lies on the axis of parabola. We are given the coordinates of vertex and focus. Hence, we can find the equation of the axis of the parabola.
On observing the coordinates of the vertex and focus of the parabola, we can notice that the y coordinate of both the points is $3$ . Hence, we can say that the axis of the parabola is
$y = 3$ .
So, we can conclude that the required parabola is facing rightwards as in the figure and the axis of the parabola is $y = 3$ .
So, the equation of the required parabola is of the form
${\left( {y - k} \right)^2} = 4a\left( {x - h} \right)$ where $\left( {h,k} \right)$ are the coordinates of the vertex of parabola.
So, we have,
${\left( {y - 3} \right)^2} = 4a\left( {x - 2} \right)$
Now, we have to find the value of a.
We know that the distance between the vertex of the parabola and focus is a.
So, distance between vertex and focus
$= \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
$\Rightarrow \sqrt {{{\left( {6 - 2} \right)}^2} + {{\left( {3 - 3} \right)}^2}}$
$\Rightarrow \sqrt {{{\left( 4 \right)}^2} + {{\left( 0 \right)}^2}}$
$\Rightarrow 4$ units
So, the value of a is $4$ .
Hence, we get the equation of the parabola as ${\left( {y - 3} \right)^2} = 16\left( {x - 2} \right)$
So, the correct answer is “ ${\left( {y - 3} \right)^2} = 16\left( {x - 2} \right)$ ”.

Note : The given question is a typical problem of equations of conic sections such as parabola and also involve basic understanding of elementary coordinate geometry. Such problems illustrate the interdependence of mathematical ideas and topics on each other. Care should be taken while doing the calculations.