Question

What is the equation of a vertical line passing through the point (-5, -1)?

Answer 1

Write the general form of a straight line that is parallel to the y axis given as x = k, where k is a constant. The absolute value of k is the distance of the line from the y axis. Substitute the x coordinate in the assumed equation to get the equation of the vertical line.

Complete step by step solution:
Here we have been given a point (-5, -1) and we are asked to find the equation of a vertical line passing through this point.
Now, vertical line means the line is parallel to the y axis or perpendicular to the x axis. We know that the equation of a line parallel to the y axis is given as x = k where k is a constant. This constant depends on the distance of the line from the y axis and the quadrant in which the point lies through which the line is passing.
Let us come to the question. The given point is (-5, -1) so it lies in the third quadrant and the x coordinate is -5 that means the distance of the vertical line that will pass through this point will be 5 units toward the left side of the y axis. So the equation of this line will be given as:
$\begin{aligned} & \Rightarrow x=-5 \\\ & \therefore x+5=0 \\\ \end{aligned}$
Hence, the equation of the vertical line is x + 5 = 0.

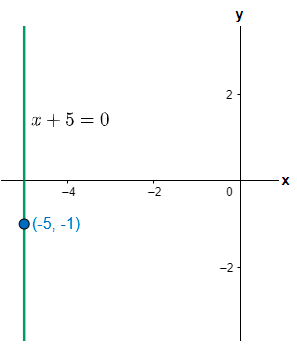
Note: Note that if we are asked to find the horizontal line passing through the above point then we will assume it as y = k and this time we need to substitute the value of y coordinate of the point as k will denote the distance of the line from the x axis above or below. The slope of a horizontal line is 0 and that of a vertical line is infinite.