Question

What is the equation for the line of symmetry for the graph of the function $y=-4{{x}^{2}}+6x-8$ ?

Answer 1

First of all, we should try to find the orientation of this given parabola. Then, we must find the maximum point for downward facing and minimum point for upward facing parabola. With the help of this point and slope information from the orientation, we can write the equation of line of symmetry.

Complete step-by-step solution:
We have the equation, $y=-4{{x}^{2}}+6x-8$.
By seeing the equation, we can easily tell that this is an equation of parabola.
Also, we don’t have any term involving $xy$ in our equation. So, we can say that this is either a horizontal or a vertical parabola. But we have a quadratic equation in x, so we can say that we are given a vertical parabola.
We know that the general equation of a parabola is $y=a{{x}^{2}}+bx+c$, and if $a>0$ the parabola is upward facing, and in case of $a<0$ the parabola is downward facing.
Here, in this question, $a=-4$ and so the parabola is downward facing.
We also know that the axis of a parabola is its axis of symmetry. And so, we will find the axis of the given parabola.
In cases of downward facing parabola vertical parabola, the maximum point will be the vertex of parabola.

So, let us find $\dfrac{dy}{dx}$ and equate it to zero.
$\dfrac{dy}{dx}=\dfrac{d}{dx}\left( -4{{x}^{2}}+6x-8 \right)$
$\Rightarrow \dfrac{dy}{dx}=-8x+6$
So, now we have,
$-8x+6=0$
Hence, we get $x=\dfrac{3}{4}$.
Now, let us verify whether is maximum or not,
$\dfrac{{{d}^{2}}y}{d{{x}^{2}}}=-8$
Here, $\dfrac{{{d}^{2}}y}{d{{x}^{2}}}<0$, so y is maximum at $x=\dfrac{3}{4}$.
Now, let us find this maximum value,
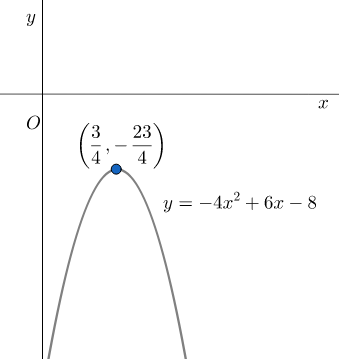
$y=-4{{x}^{2}}+6x-8$ and $x=\dfrac{3}{4}$
Thus, we get,
$y=-4{{\left( \dfrac{3}{4} \right)}^{2}}+6\left( \dfrac{3}{4} \right)-8$
$\Rightarrow y=-\dfrac{9}{4}+\dfrac{18}{4}-8$
$\Rightarrow y=-\dfrac{23}{4}$
We know that since this is a vertical parabola, the axis will be parallel to y-axis.
So, a line parallel to y-axis and passing through the point $\left( \dfrac{3}{4},-\dfrac{23}{4} \right)$ is $x=\dfrac{3}{4}$.
Hence, the line $x=\dfrac{3}{4}$ is the line of symmetry for $y=-4{{x}^{2}}+6x-8$.

Note: We must remember that for a parabola $y=a{{x}^{2}}+bx+c$ the axis of symmetry will be given by the equation $x=-\dfrac{b}{2a}$. This is a direct formula, which may be very useful for us, and so we must memorize this equation for the axis of symmetry.