Question
Question: What is the energy stored in the capacitor between the terminals a and b of the network shown in the...
What is the energy stored in the capacitor between the terminals a and b of the network shown in the figure?
Capacitance of each capacitor C=1μF)
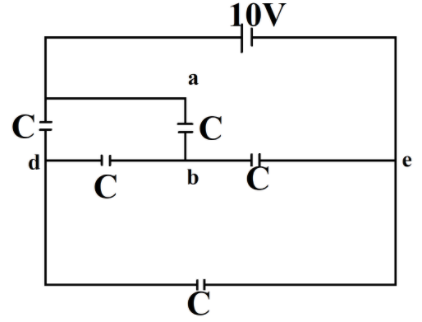
A. 12.5μJ
B. Zero
C. 25μJ
D. 50μJ
Solution
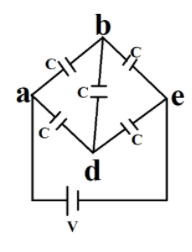
If you look closely at the diagram, you will notice that there is a wheatstone network in here. It is a balanced Wheatstone network. So, it can easily be solved using the concept of a wheatstone bridge. In a balanced Wheatstone Bridge, It is said that both sides of the parallel bridge network are balanced since the voltage at point C is equal to the voltage at point D, with zero being the difference.
Formula used:
For solving this question, we will be using the formula
Q = CV
Step by step solution:
First, let us redraw the diagram to make it a Wheatstone network
Now, Applying the concept of the balanced Wheatstone bridge,
Ceq=C
Now, The Charge on capacitor between the terminals a and b
2Q=2CV
Now, for the energy stored in the capacitor between a and b,
=2C(2Q)2=8CQ2
Now, using
Q = CV
We have
⇒Q=8CC2V2
⇒Q=8CV2
Now, as
C=1μF
And, V = 10 V
Takin the given values,
⇒U=2C(1×10−6)×102
⇒U=8100×10−6
⇒U=12.5μJ
So, the energy stored in the capacitor between the terminals a and b of the network shown in the figure will be 12.5μJ, i.e., Option – A.
Note:
The network (or bridge) of Wheatstone is a circuit for indirect resistance calculation by a null reference approach relative to an established normal resistance. It consists of four R1, R2, R3 and R4 resistors connected to a quadrilateral ABCD. The Wheatstone bridge was created by the British Scientist, mathematician and physicist, Samuel Hunter Christie in 1843.
