Question

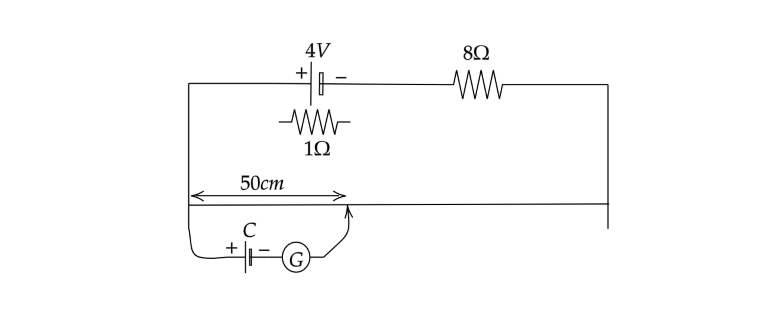
What is the emf of the cell C in the circuit shown in figure, if the deflection in the galvanometer is zero, the resistance of the wire is $3\Omega$, the length of the wire is $100cm$?

$\left( A \right)0.25V$
$\left( B \right)0.50V$
$\left( C \right)0.75V$
$\left( D \right)1.00V$

Answer 1

Here we have to use the meter bridge principle to solve this problem. First we use Kirchhoff voltage law to find the current flowing through the meter bridge circuit. Now zero deflection of the galvanometer shows that voltage across the cell C is equal to the voltage across the $50cm$ wire. Now using this we can find the emf of the cell.

Complete step by step answer:
As per the given problem we have the defection in the galvanometer is zero, the resistance of the wire is $3\Omega$, the length of the wire is $100cm$.
Let I is the amount of current flowing in the circuit.
And r is the internal resistance of the $4V$ cell as gibe in the figure.
$3\Omega$ is the resistance of the $100cm$ wire.
Now taking a loop across the meter bridge we will get,
Using KVL in the loop ABCD, we have,

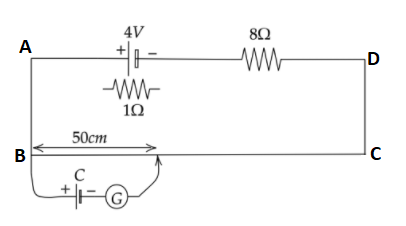
$4 - Ir - 8I - 3I = 0$
Now putting internal resistance we will get,
$4 - I - 8I - 3I = 0$
$\Rightarrow 4 - 12I = 0$
Or, $I = \dfrac{1}{3}A$
As the galvanometer shows zero deflection we can write,
Voltage across $50cm$ wire is equal to voltage across the cell C.
${V_{50}} = {V_C}$
We know voltage is the product of current and resistance.
${V_C} = {I_{50}}{R_{50}}$
As we know,
$100cm \to 3\Omega$
$1cm \to \dfrac{3}{{100}}\Omega$
Now we can write,
$50cm \to \dfrac{3}{{100}} \times 50\Omega$
And also, $I = {I_{50}} = \dfrac{1}{3}\Omega$
Now putting the values in above equation we will get,
${V_C} = \dfrac{1}{3}\left( {\dfrac{3}{{100}} \times 50} \right)V$
Now on cancelling and on further solving we will get,
${V_C} = 0.5V$

Therefore the correct option is (B).

Note:
Remember that the meter bridge is based on the principle of Wheatstone bridge circuit and which states if any point or length in the ratio of two resistance is equal to the ratio of another two resistance then there shall be zero flow of current and the galvanometer connected in it shows zero deflection.