Question: What is the electric flux through a cube of side 1cm which encloses an electric dipole?...

Question

What is the electric flux through a cube of side 1cm which encloses an electric dipole?

Answer 1

Solution

Hint: We can find the electric field orientation using Gauss's law. Electric flux is the number of field lines passing through a given surface. Gauss’s law deals with the electric flux through a closed surface.

Complete step by step answer:

Gauss’s law states that,

“The net electric flux through any hypothetical closed surface is equal to $\dfrac{1}{{{\varepsilon }_{0}}}$ times the net charge within that closed surface.”

Hence, Gauss’s law can be expressed as:
${{\phi }_{E}}=\dfrac{Q}{{{\varepsilon }_{0}}}$

Where,
${{\phi }_{E}}$ is the electric flux through a closed surface
$Q$ is the total charge enclosed by the surface
${{\varepsilon }_{0}}$ di-electric constant of that medium

So, the net charge in the above question is zero.

Electron dipole is a positive and negative charge of equal magnitude at a specific distance.

Hence, the total charge inside the cube is zero.
So, if we apply Gauss’s law, then the net electric field through the cube is zero.

Let’s look at the reason behind this zero-electric flux.

We can take any of the 6 sides of the box to explain this.

Let’s look at the following diagram:

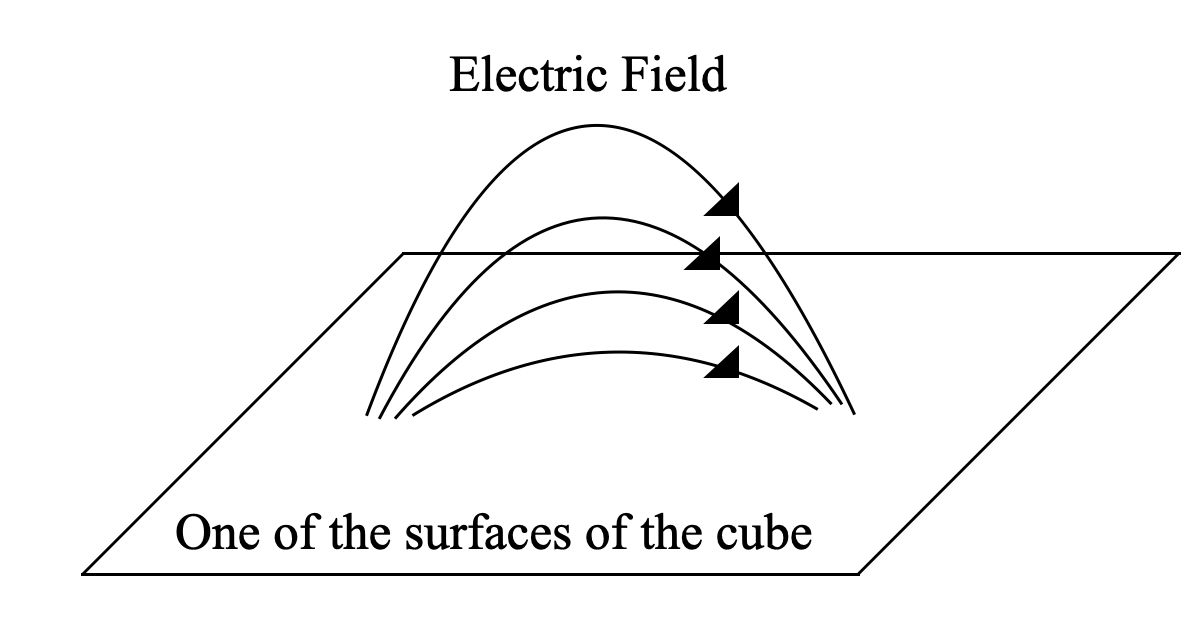
In an electric dipole the electric field lines start at the positive charge and end at the negative charge. So, if we check the electric field lines originating from the positive charge, they will contribute a positive flux at the surface of the cube.

However, the same field lines will have to cross the side again to end at the negative pole. Hence, it will contribute to the same magnitude of negative electrical flux.

Hence, positive and electric flux cancel each other to have a net electric flux of zero.

Note: Gauss’s law is one of the fundamental laws of electrodynamics. This law can be applied to gravitational force of attraction or magnetic force as well. Coulomb's law in electrostatics and Newton’s law in gravity can be derived from Gauss’s law. However, the constant is different in those two cases.