Question
Question: What is the effective resistance between the points \(A\) and \(B\) in the network shown below? ...
What is the effective resistance between the points A and B in the network shown below?
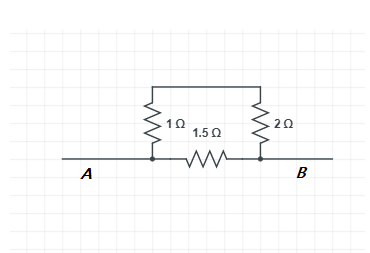
Solution
The given figure is a combination of resistances which are connected parallel and series. In a series connection, the same amount of current flows through the circuit. While in parallel circuit, same amount of voltage flows through the circuit.
Formula used:
Rs=R1+R2 and Rp1=R11+R21
Complete answer:
We know that Ohm’s law gives the relationship between voltage V, current I and resistance R. It is given as V=IR when the temperature is constant.
We also know that, since current in the series connection is constant or same amount of current flows through the circuit , then the effective resistance Rs is given by Rs=R1+R2
Also, since voltage in the parallel connection is constant same amount of voltage flows through the circuit, then the effective resistance Rp is given by Rp1=R11+R21
Since the same amount of current flowing through the resistances R1=1Ω and R2=2Ω then, the resistances R1=1Ω and R2=2Ω are in series connection and the effective resistance is given by Rs=1+2=3Ω
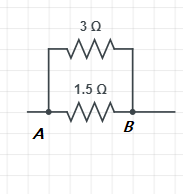
Similarly, since the same amount of voltage flowing through the resistances R1=1.5Ω and R2=3Ω then, the resistances R1=1.5Ω and R2=3Ω are in parallel connection and the effective resistance is given by Rp1=1.51+31=32+1=33=1Ω
Thus, the resultant resistance obtained is 1Ω
So, the correct answer is “Option A”.
Note:
Since it is not possible, every time to calculate the current or voltage. Another, easy way to say if the resistances are in series or parallel connections is by observing the circuit diagram. If two or more resistances have one common point then, they are said to be in series circuit. If two or more resistances have two common points then, they are said to be in parallel circuit.
