Question
Question: What is the effective capacitance between points X and Y? 
A. 24μF
B. 18μF
C. 12μF
D. 6μF
Solution
- Hint – The given circuit is a Wheatstone bridge circuit and here C3C1=C4C2 . Thus, no charge flows through the capacitor C5=20μF . Use this to solve the question.
Formula used - C3C1=C4C2 , C13=C1+C3C1×C3 , C24=C2+C4C2×C4 , CXY=C13+C24
Complete step-by-step solution -
The circuit given in the question is a Wheatstone bridge circuit and here C3C1=C4C2 . Also, no charge flows through the capacitor C5=20μF .
Drawing the equivalent circuit-
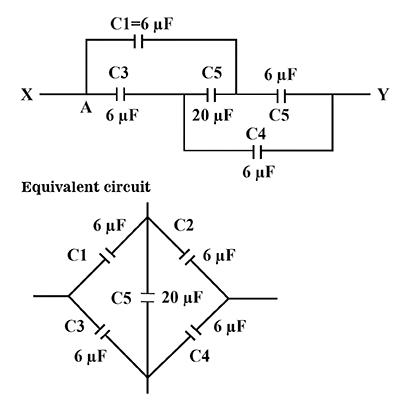
Now, we can see that C1 and C3 are in series, so the equivalent capacitance will be-
C13=C1+C3C1×C3
Putting the values of C1=6μF,C3=6μF , we get-
C13=6+66×6=3μF
Also, C2 and C4 are in series, so the equivalent capacitance will be-
C24=C2+C4C2×C4
Putting the values of C2=6μF,C4=6μF , we get-
C24=6+66×6=3μF
Now, C13 and C24 are in parallel, so now the equivalent of this combination will give us the capacitance between the points X and Y.
So, finding the value of the capacitance between X and Y.
CXY=C13+C24
putting the values, we get-
CXY=3+3=6μF
Therefore, the effective capacitance between points X and Y is 6μF .
Hence, the correct option is D.
Note- Whenever solving such types of questions, first draw the equivalent circuit which makes it easier to solve. Also, as mentioned in the solution, the given circuit is a Wheatstone bridge circuit, so as we know, a Wheatstone bridge is an electrical circuit used to measure an unknown capacitance by balancing two legs of a bridge circuit, one leg of which includes the unknown. So, using this concept we have found out the capacitance between the given points.
