Question

What is the eccentricity of a hyperbola?

Answer 1

Eccentricity of a hyperbola is defined as $e=\sqrt{1+\dfrac{{{b}^{2}}}{{{a}^{2}}}}$ , where a is the length of semi major axis and b is the length of semi minor axis. For a hyperbola, the value of eccentricity e is always greater than 1, that is, e > 1.

Complete step by step solution:
We know that hyperbola is a collection of a set of points, whose difference of distances from two fixed points is a positive constant. These fixed points are called foci, and are shown as A and A’ in the figure below. Here, the origin is the centre of the hyperbola, and the intersecting points of the line joining the two foci and the conic section are called vertices of the hyperbola.

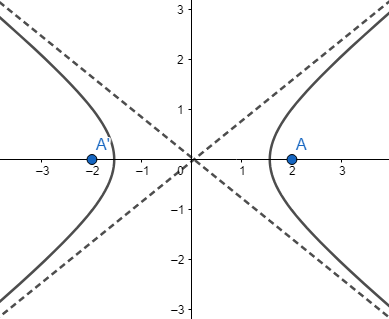
We are well aware that hyperbola is a conic section, and has two branches.
Hyperbola can also be defined in terms of eccentricity, but for that, we first need to understand what eccentricity means.
Eccentricity is a measure of the deviation occurred in the circularity of any conic section.
So mathematically, we can define eccentricity of any conic section as
$e=\dfrac{c}{a}$
Where e is the eccentricity of the conic section,
c is the distance between centre and the focus, and
a is the distance between centre and the vertex.
Now, we can define hyperbola in terms of eccentricity as the conic section whose eccentricity is greater than 1, that is, e > 1.
We know that the general equation of a hyperbola is
$\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ ,
where, a is the length of semi major axis,
and b is the length of semi minor axis.
So, in other words we can define hyperbola as a conic section in which the distance from a fixed point is greater than the distance from a fixed line, called the directrix.
Hence, for a hyperbola, eccentricity e > 1.
We know that eccentricity for a hyperbola is expressed as
$e=\sqrt{1+\dfrac{{{b}^{2}}}{{{a}^{2}}}}$

Note: We should not consider the a in eccentricity $e=\dfrac{c}{a}$ and the a in general equation of hyperbola $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ as two different quantities. They both represent the same quantity.
We must also note that the above general equation of hyperbola is valid when the centre of the hyperbola is the origin (0,0).