Solveeit Logo
Login

Question

Question: What is the eccentric angle in the first quadrant of a point on the ellipse \(\dfrac{{{x^2}}}{{10}} ...

What is the eccentric angle in the first quadrant of a point on the ellipse x210+y28=1\dfrac{{{x^2}}}{{10}} + \dfrac{{{y^2}}}{8} = 1 at a distance 3 units from the centre of the ellipse?
(A). π6\dfrac{\pi }{6}
(B). π4\dfrac{\pi }{4}
(C). π3\dfrac{\pi }{3}
(D). π2\dfrac{\pi }{2}

Explanation

Solution

Hint- In such types of questions, just follow the simple approach first take the parametric equation of ellipse x2a2+y2b2=1\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1 centred at origin and find the distance of x=acos⁡θ,y=bsin⁡θx = a\cos \theta ,y = b\sin \theta point in the first quadrant from the origin and then equate that to the given distance to get the required value of θ\theta i.e. the eccentric angle.

Complete step-by-step solution -
Let us suppose the point PP is on the ellipse given.

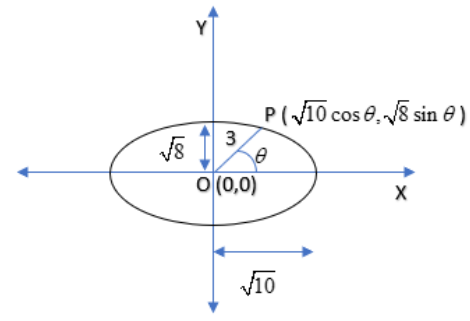
Now we have a2=10,b2=8{a^2} = 10,{b^2} = 8 so we have a=10,b=8a = \sqrt {10} ,b = \sqrt 8
We have the parametric equation of the ellipse as x=acos⁡θ,y=bsin⁡θx = a\cos \theta ,y = b\sin \theta and here x=10cos⁡θ,y=8sin⁡θx = \sqrt {10} \cos \theta ,y = \sqrt 8 \sin \theta
Now, we know that the distance formula to calculate distance between two points say A (x1,y1)(x_1, y_1) and B (x2,y2)(x_2, y_2) which is d=(x2−x1)2+(y2−y1)2d = \sqrt {{{(x_2 - x_1)}^2} + {{(y_2 - y_1)}^2}}
Here the two points are P(10cos⁡θ,8sin⁡θ)P(\sqrt {10} \cos \theta ,\sqrt 8 \sin \theta ) and O (0, 0)
So, d=(0−10cos⁡θ)2+(0−8sin⁡θ)2d = \sqrt {{{\left( {0 - \sqrt {10} \cos \theta } \right)}^2} + {{\left( {0 - \sqrt 8 \sin \theta } \right)}^2}}
⇒d=(−10cos⁡θ)2+(−8sin⁡θ)2\Rightarrow d = \sqrt {{{\left( { - \sqrt {10} \cos \theta } \right)}^2} + {{\left( { - \sqrt 8 \sin \theta } \right)}^2}}
⇒d=10cos⁡2θ+8sin⁡2θ\Rightarrow d = \sqrt {10{{\cos }^2}\theta + 8{{\sin }^2}\theta }
Now, d = 3 as given in the question so we get,
⇒3=10cos⁡2θ+8sin⁡2θ\Rightarrow 3 = \sqrt {10{{\cos }^2}\theta + 8{{\sin }^2}\theta }
Squaring both sides, we get,
⇒32=10cos⁡2θ+8sin⁡2θ\Rightarrow {3^2} = 10{\cos ^2}\theta + 8{\sin ^2}\theta
⇒9=10cos⁡2θ+8sin⁡2θ\Rightarrow 9 = 10{\cos ^2}\theta + 8{\sin ^2}\theta
Now we know that cos⁡2θ=1−sin⁡2θ{\cos ^2}\theta = 1 - {\sin ^2}\theta
⇒9=10(1−sin⁡2θ)+8sin⁡2θ\Rightarrow 9 = 10(1 - {\sin ^2}\theta ) + 8{\sin ^2}\theta
⇒9=10−10sin⁡2θ+8sin⁡2θ\Rightarrow 9 = 10 - 10{\sin ^2}\theta + 8{\sin ^2}\theta
⇒10sin⁡2θ−8sin⁡2θ=10−9\Rightarrow 10{\sin ^2}\theta - 8{\sin ^2}\theta = 10 - 9
⇒2sin⁡2θ=1\Rightarrow 2{\sin ^2}\theta = 1
⇒sin⁡2θ=12\Rightarrow {\sin ^2}\theta = \dfrac{1}{2}
⇒sin⁡θ=12\Rightarrow \sin \theta = \dfrac{1}{{\sqrt 2 }}
We know that sin⁡(π4)=12\sin \left( {\dfrac{\pi }{4}} \right) = \dfrac{1}{{\sqrt 2 }} in the first quadrant.
So, we have θ=π4\theta = \dfrac{\pi }{4}
Hence, the eccentric angle in the first quadrant of a point on the ellipse x210+y28=1\dfrac{{{x^2}}}{{10}} + \dfrac{{{y^2}}}{8} = 1 at a distance 3 units from the centre of the ellipse is θ=π4\theta = \dfrac{\pi }{4}
∴\therefore Option B. π4\dfrac{\pi }{4} is the correct answer.

Note- In such types of questions, just keep in mind the distance formula to calculate the distance between two points i.e. for two points say two points say A (x1,y1)(x_1, y_1) and B (x2,y2)(x2, y2) distance is d=(x2−x1)2+(y2−y1)2d = \sqrt {{{(x_2 - x_1)}^2} + {{(y_2 - y_1)}^2}} and also keep in mind the parametric equation of ellipse as x=acos⁡θ,y=bsin⁡θx = a\cos \theta ,y = b\sin \theta .