Question

What is the easiest way to solve the ambiguous case in terms of the law of sines?

Answer 1

First we will understand the condition in which the ambiguous case in the law of sines arises. Now, we will consider an example of a triangle in which we will assume the length of two sides and angle other than in between the two sides. We will find the measure of the other angle and check if there can be another possibility using the fact that $\sin \left( {{180}^{\circ }}-\theta \right)=\sin \theta$. We will see the process used to solve such problems. Use the formula $\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$ where a, b and c are the sides opposite to the angles A, B and C respectively.

Complete step by step solution:
Here we have been asked to determine the easiest way to solve an ambiguous case using the law of sines. First we need to understand the meaning of ambiguous cases.
Now, an ambiguous case in the Law of sines arises where we have been provided with the length of two sides of a triangle and an angle other than in between the two sides. We have to determine the other angle and check if there is more than one possible value of the angle. Let us understand this with the help of an example.

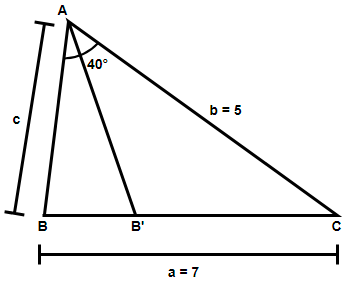
In the above figure we have considered a triangle ABC with the sides a = 7 and b = 5. Also, we have an angle given as $\angle A={{40}^{\circ }}$. Clearly we can see that this is an ambiguous case because the angle whose measure is given does not lie between the two sides whose length is given. So, using the law of sines, we can write: -
$\Rightarrow \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$
Here, a, b and c are the sides opposite to the angles A, B and C respectively. Substituting the values given we get,
$\Rightarrow \dfrac{7}{\sin {{40}^{\circ }}}=\dfrac{5}{\sin B}=\dfrac{c}{\sin C}$
Equating the first two terms we get,
$\begin{aligned} & \Rightarrow \dfrac{7}{\sin {{40}^{\circ }}}=\dfrac{5}{\sin B} \\\ & \Rightarrow \sin B=5\times \dfrac{\sin {{40}^{\circ }}}{7} \\\ \end{aligned}$
Using the value $\sin {{40}^{\circ }}$ using the calculator and calculation the angle B we get,
$\begin{aligned} & \Rightarrow \dfrac{7}{\sin {{40}^{\circ }}}=\dfrac{5}{\sin B} \\\ & \Rightarrow \sin B=5\times \dfrac{\sin {{40}^{\circ }}}{7} \\\ & \Rightarrow B\approx {{27.33}^{\circ }} \\\ \end{aligned}$
We know that $\sin \left( {{180}^{\circ }}-\theta \right)=\sin \theta$ so it may be possible that angle B is obtuse, i.e. $\left( {{180}^{\circ }}-{{27.33}^{\circ }} \right)={{152.67}^{\circ }}$. So, let us see the steps to solve this ambiguous case.
Step (1): -After finding the two possible values of angle B we need to add this obtuse angle with the angle given, i.e. angle A.
Step (2): - In case the sum is equal to or greater than 180 degrees the construction triangle is not possible because we know that the sum of all the interior angles of a triangle is 180 degrees.
Step (3): - In case the sum is less than 180 degrees the two values of the angle (one obtuse and the other acute can be possible).
In the above example taking the sum of obtuse angle B as angle A we get,
$\Rightarrow \left( {{152.67}^{\circ }}+{{40}^{\circ }} \right)={{194.67}^{\circ }}$
Here the sum is greater than 180 degree so the obtuse angle B is not possible. Hence, we can conclude that the measure of angle B is ${{27.33}^{\circ }}$.

Note: Once the measure of angle B is obtained we can easily determine the remaining side angle. You must remember the angle sum property of a triangle. Note that the formula $\sin \left( {{180}^{\circ }}-\theta \right)=\sin \theta$, where $\theta$ is acute, corresponds to the fact that the sine of an angle is positive in first quadrant and second quadrant both. You may take other examples to see various situations arising.