Question

What is the domain of the function $\csc x$?

Answer 1

In this problem we need to calculate the domain of the given function. We know that the domain is the all set of values for which the given function is valid and gives real values as output. We can observe that the given function is a trigonometric function. From basic trigonometric definitions we can write the trigonometric function $\csc x$ as $\csc x=\dfrac{1}{\sin x}$. From this we can say this as $\csc x$ is the inverse function of $\sin x$. So, the domain of the function $\csc x$ is the reverse or inverse of the domain of $\sin x$ function.

Complete step by step answer:
Given function $\csc x$.
We know that the domain is the set of values of $x$ for which the given function that means $\csc x$ is valid and should be given real value as output.
From the basic definitions of the trigonometry, we can write the given function as
$\csc x=\dfrac{1}{\sin x}$
From the above equation we can say that the trigonometric function $\csc x$is the inverse function of the trigonometric function $\sin x$.
We know that the function $\sin x$ is valid for all real values. We can observe that function $\sin x$ will give $0$ for all $x=k\pi$. If the value of $\sin x$ is $0$, then the value of $\csc x$ will become infinite that means the function is invalid.
Hence the domain of the function $\csc x$ is $x\ne kZ$.

Note: We can also find the domain of the function by observing the graph of the given function. The graph of the function $\csc x$ as

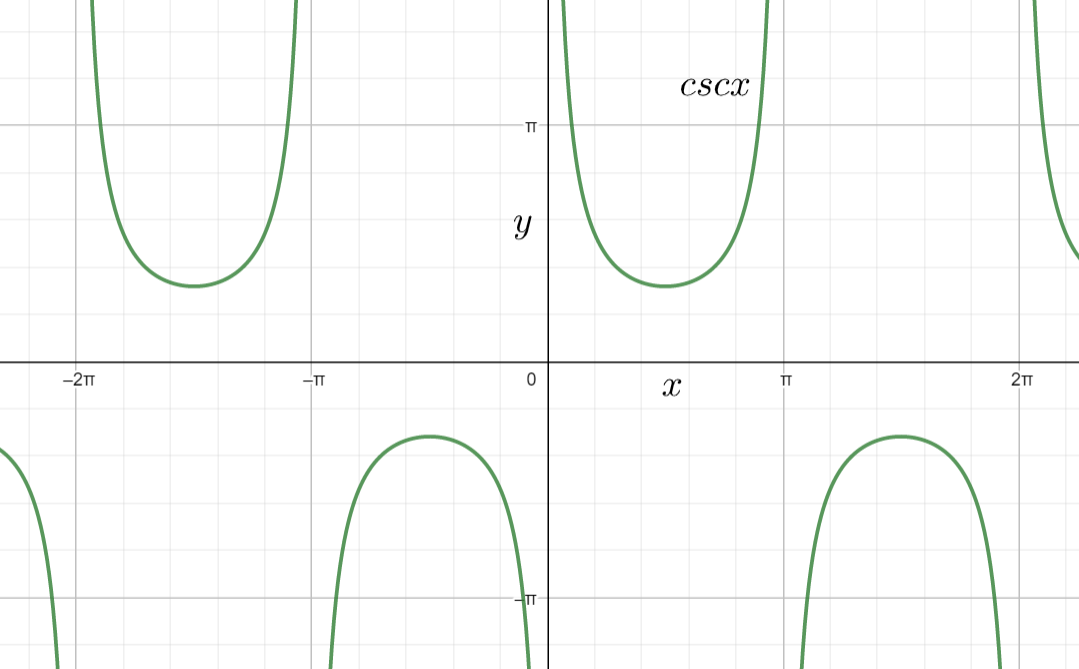
From the above graph also, we can say that the function $\csc x$ is invalid at $k\pi$ where $k=\pm 1,\pm 2,\pm 3,....$. Hence the domain of the function $\csc x$ is $x\ne kZ$.