Question

What is the domain of $\tan x$ ?

Answer 1

We can define that, the domain of a function is the complete step of possible values of the independent variable. So, we can say that the domain is the set of all possible ‘x’ values which will make the function ‘work’ and will give the output of ‘y’ as a real number. We remember that, $\tan x=\dfrac{\sin x}{\cos x}$, therefore you will have a vertical asymptote whenever $\cos =0$. $\cos =0$ for every odd multiple of $\dfrac{\pi }{2}$. If you plug $y=\tan \left( x \right)$ into a graphing calculator, you will see that the ends of each section continue to infinitely along the y-axis.

Complete step by step answer:
The domain of the expression is all real numbers except where the expression is undefined, which means there are no real numbers that make the expression undefined. It is given that, $y=\tan \left( x \right)$. Now let’s define the domain of the function,
$y=\tan x$
As we know that,
$\tan x=\dfrac{\sin x}{\cos x}$
It means the $\tan x$ will be defined for all values except the values that will make $\cos x=0$ because a function cannot be defined with a zero denominator. So, the domain of $f\left( x \right)=\tan \left( x \right)$ will be,
$R-\dfrac{\left( 2n+1 \right)\pi }{2}$ , where $n\in z$
We will now find the domain by $\tan x$ curve. So,
$y=f\left( x \right)=\tan x$

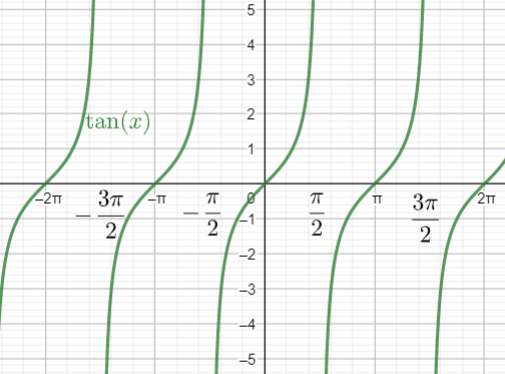
The trigonometric values of $\tan \theta$ at different angles is,

$\theta$	0	$\dfrac{\pi }{4}$	$\dfrac{\pi }{2}$	$-\dfrac{\pi }{4}$	$-\dfrac{\pi }{2}$
$\tan \theta$	0	1	$\infty$	-1	$-\infty$

The curve of $\tan x$ shows that on the odd values of $\dfrac{\pi }{2}$, the value of $\tan \theta$ will be infinite.
Therefore, the domain of $\tan x$ will be,
Domain: R-\left\\{ \dfrac{\left( 2n+1 \right)\pi }{2} \right\\}

Note: We must know the trigonometry concepts to solve this question. The domain where the x value ranges and the range where the y value rages. Here the function is a form of trigonometric function.