Question

What is the domain of $\sin (\arcsin x)$?

Answer 1

If $f:X \to Y$ such that $f(x) = y$ is one-one and onto, then we can define a unique function $g:Y \to X$ such that $g(y) = x$, where $x \in X$ and $y = f(x),y \in Y$. Here, the domain of $g =$ range of $f$ and the range of $g =$ domain of $f$. The function g is called the inverse of $f$ and is denoted by $f$. Further, $g$ is also one-one and onto and inverse of $g$ is $f$. Thus, ${g^{ - 1}} = {({f^{ - 1}})^{ - 1}} = f$. We also have

(fo{f^{ - 1}})(y) = f({f^{ - 1}}(y)) = f(x) = y \\\ $$ To find: Domain of $$\sin (\arcsin x)$$or $$sin\left( {si{n^{ - 1}}x} \right)$$ **Complete step-by-step solution:** As we know that the notation $$f:X \to Y$$ means that $f$ is a function from $$X$$ to $Y$. $$X$$ is called the domain of $f$ and $Y$ is called the co-domain of $f$. Given an element $$x \in X$$, there is a unique element $y$ in $Y$ that is related to $x$. The unique element $y$ to which $f$ relates $x$ is denoted by $$f\left( x \right)$$ and is called $f$ of $x$, or the value of $f$ at $x$, or the image of $x$ under $f$. The set of all values of $$f\left( x \right)$$ taken together is called the range of $f$ or image of $$X$$ under $f$ $x$| ${\sin ^{ - 1}}x$ | $\sin \left( {{{\sin }^{ - 1}}x} \right)$ ---|---|--- $$ - 1.5$$ | undefined| undefined $$ - 1$$ | $$ - \dfrac{\pi }{2}$$| $$ - 1$$ $$ - 0.5$$ | $$ - \dfrac{\pi }{6}$$| $$ - 0.5$$ $$0$$ | $$0$$| $$0$$ $$0.5$$ | $$\dfrac{\pi }{6}$$| $$0.5$$ $1$| $$\dfrac{\pi }{2}$$| $1$ $$1.5$$ | undefined| undefined Since, we have $$y = \sin (\arcsin x) = \sin ({\sin ^{ - 1}}x) = x$$ Therefore, the domain of $$\sin (\arcsin x)$$ are all the defined values of $$\sin (\arcsin x)$$ in above table i.e. $$domain,x \in \left[ { - 1,1} \right]$$ 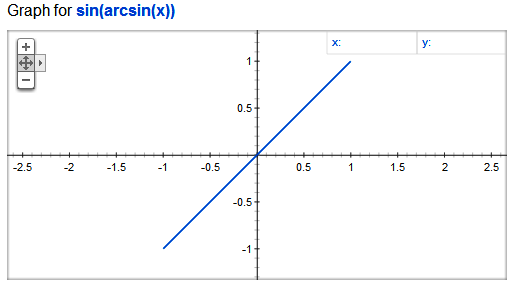 **Note:** > $${\sin ^{ - 1}}x$$ Should not be confused with $${(\sin x)^{ - 1}}$$. In fact$${(\sin x)^{ - 1}} = \dfrac{1}{{\sin x}}$$ and similarly for other trigonometric functions. > The value of inverse trigonometric functions which lies in its principal value branch is called the principal value of those inverse trigonometric functions. > The most common notation to denote these inverse trigonometric functions are by prefixing an arc before the trigonometric function (i.e.) $$arcsin\left( x \right)$$ ,$$arccos\left( x \right)$$ , $$arctan\left( x \right)$$,$${\text{ }}arc{\text{ }}sec\left( x \right)$$ > Generally in Mathematics, the inverse trigonometric functions are known as arcus function which is the inverse function of the trigonometric function. In particular, they are the inverses of the sine, cosine, tangent, cotangent, secant and cosecant functions.