Question

What is the domain and range of $y=\tan x$?

Answer 1

In this problem, we have to find the domain and range of the given function $y=\tan x$. We know that the domain of the function $y=\tan x$ is all real numbers except the values where $\cos x$ is equal to zero, i.e. the values $\dfrac{\pi }{2}+\pi n$ for all integers n. The range of the tangent function is all real numbers. We can draw the graph for the given function and write the domain and the range.

Complete step by step solution:
Here we have to find the domain and the range of the given function $y=\tan x$.
We know that the domain of the function $y=\tan x$ is all real numbers except the values where $\cos x$ is equal to zero, i.e. the values $\dfrac{\pi }{2}+\pi n$ for all integers n as we know that $\tan x=\dfrac{\sin x}{\cos x}$ which is not defined when denominator is 0.
The range of the tangent function is all real numbers.
If we plug $y=\tan x$ in a graphing calculator, we can see that the ends of each section continue on infinitely along the y-axis.

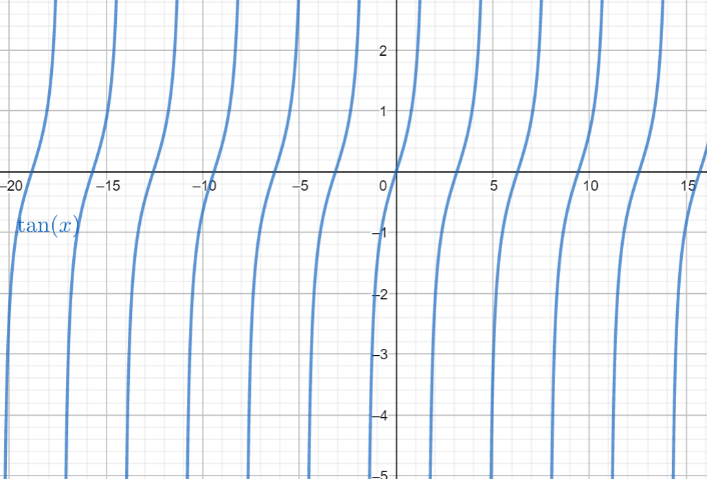
Therefore, the domain of the given function $y=\tan x$ is $\left( \theta \ne k\dfrac{\pi }{2},\text{ where k is an integer} \right)$.
The range is $\left( -\infty ,\infty \right)$.

Note: We should always remember that the function $y=\tan x$ is all real numbers except the values where $\cos x$ is equal to zero, i.e. the values $\dfrac{\pi }{2}+\pi n$ for all integers n as we know that $\tan x=\dfrac{\sin x}{\cos x}$ which is not defined when denominator is 0. The range of the tangent function is all real numbers.