Question

What is the domain and range of $y={{e}^{x}}$?

Answer 1

In this question we have been given with an exponential function $y={{e}^{x}}$ for which we have to find the domain and the range. The domain of a function is the subset of the set $\mathbb{R}$, for which all the operations in the functions exist and the range of a function is the set of function values whenever an element from the domain is substituted in the function.

Complete step by step solution:
We have the function given to us as:
$\Rightarrow y={{e}^{x}}$
We know that $e$ is a positive real number which is a constant therefore, it can be raised to any power which implies the domain is not limited to any specific subset of $\mathbb{R}$. The domain of the function is $\mathbb{R}$ itself. Therefore, the domain is $\left( -\infty ,+\infty \right)$.
Now the range of a function is the set of all the values of the function when any number or term from the domain is substituted in it.
We know that $e$ is a positive real constant therefore, any number substituted from the domain $\mathbb{R}$ will yield a positive number when substituted in place of $x$ in the given function.
It is to be noted that $e$ raised to any number will never yield $0$ because if the power is equal to $0$, the base must also be equal to $0$, and the exponent must be different from $0$. So, we get the range as all positive real numbers without $0$.
Therefore, we have the range as $\left( 0,+\infty \right)$ for the function.
We can see the function as:

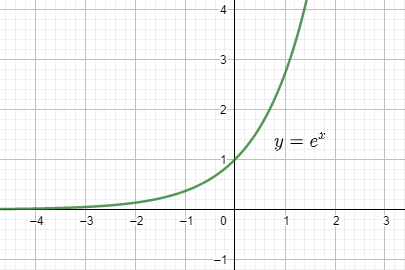
Note: It is to be remembered that a general rule of exponential functions is that the domain of the function is $\left( -\infty ,+\infty \right)$ and the range of a function is $\left( 0,+\infty \right)$. The domain $\mathbb{R}$, is the set of real numbers which consists of all numbers including positive, negative, fractions and decimals. The number $e$ is an irrational number which has a value of $2.7182....$.