Question

What is the domain and range of $y = \dfrac{{{x^2} - x - 1}}{{x + 3}}$?

Answer 1

Definition of a function:
Let $A\,\,\& \,B$ be any two non-empty sets, a rule by which every elements in the set $A$ is assigned to some unique elements in the set $B$ and it is denoted as $f:A \to B$. Also we can define that $f$ is a function from $A$ into $B$ and it is defined by $f(x) = y$.
Definition of domain of the function:
Domain of the function is defined as {D_f} = \left\\{ {x:x \in A} \right\\}, that is, all possible values of $x \in A$.
There are some restrictions in the domain of the function in which few rules are listed below.
Rules for the domain of a function:
1. Non-zero denominator in the functions:
The function is of the form: f\left( x \right) = \left\\{ {\dfrac{{P\left( x \right)}}{{Q\left( x \right)}}:Q\left( x \right) \ne 0 = O\left( x \right)} \right\\}, where O\left( x \right) = \left\\{ {O\left( x \right) = 0:x \in \mathbb{R}} \right\\} is called a zero function.
2. Non-negative square root functions:
The function is of the form: f\left( x \right) = \left\\{ {\sqrt {G\left( x \right)} :G\left( x \right) \geqslant 0} \right\\}
Definition of Range of a function:
Range of the function $f(x)$ is the graph of $f$ and is defined as {R_f} = \left\\{ {f\left( x \right):f\left( x \right) \in B,\,x \in A} \right\\}, where range of $f$ is always onto function.

Complete step-by-step solution:
From the given function, we have $y = f\left( x \right) = \dfrac{{{x^2} - x - 1}}{{x + 3}}$
The domain of $f(x)$ is x \in \mathbb{R} - \left\\{ { - 3} \right\\} or in the interval notation x \in \left( { - \infty ,\infty } \right) - \left\\{ { - 3} \right\\}
And the range of $f(x)$ is $f\left( x \right) \in \mathbb{R} - \left( { - 13.633,\, - 0.367} \right)$ as seen in the below figure.

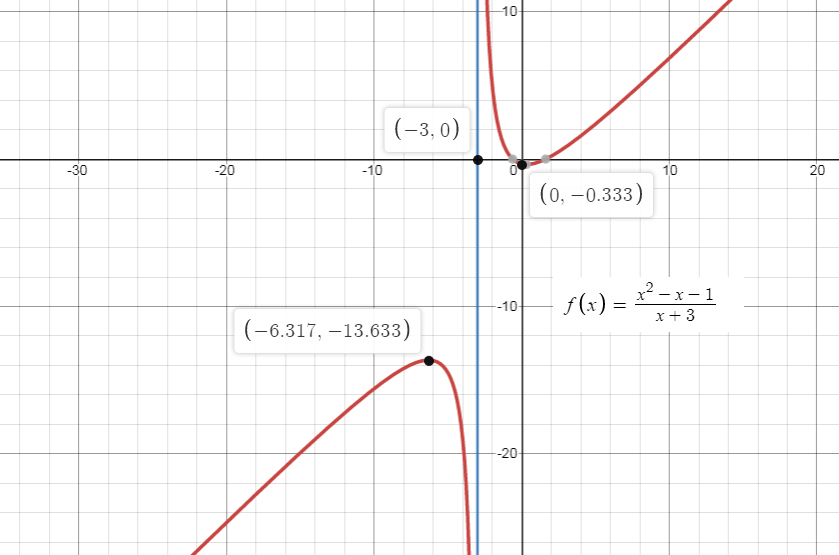
Therefore, the domain of a function $y = f\left( x \right) = \dfrac{{{x^2} - x - 1}}{{x + 3}}$ is x \in \left( { - \infty ,\infty } \right) - \left\\{ { - 3} \right\\} and the range of the function is $f\left( x \right) \in \mathbb{R} - \left( { - 13.633,\, - 0.367} \right)$.

Note: In the above graph of the function, $y = f\left( x \right) = \dfrac{{{x^2} - x - 1}}{{x + 3}}$ has a vertical asymptotes at $x = - 3$.
The domain of $f(x)$ is except one point that covers all the real line and the range of $f(x)$ is the graph of the function excluding the open intervals in which it has no pre-images.