Question

What is the domain and range of $y=-1$?

Answer 1

Firstly, when we check out the values that the function takes upon $x-axis$ or the horizontal axis are considered to be the domain of the function $y=-1$. Secondly, we are supposed to check out the values that the function takes upon the $y-axis$ or the vertical axis is considered to be the range of the function $y=-1$.

Complete step by step solution:
Now let us know more about the domain and range.
Domain: The domain is a set of all possible $x-$ values which makes the function work and will provide us with the real $y-$ values.
Range: The range is a set of all possible resulting values after we substitute all the possible $x-$values.
Now from the question, we have the function $y=-1$.
Let us find out the domain and range of $y=-1$.
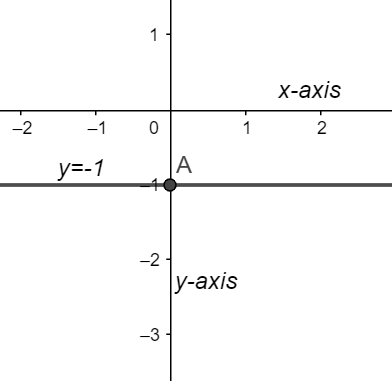
Firstly let us find out the domain of $y=-1$. We can observe that $y=-1$ is a horizontal line at $y=-1$. Now we can take all the real numbers from the horizontal axis i.e. $-\infty$ to $\infty$.
Since all the real numbers are considered, we can conclude that the domain of the function $y=-1$ is $R$.
Now let us find out the range of the function $y=-1$.
We have seen that $y=-1$ is a horizontal line at $y=-1$.So $y=-1$ takes only $-1$ upon the $y-axis$.
And hence we can conclude that the range of $y=-1$ is $\\{-1\\}$.

Note: While finding the domain we must note that the denominator cannot be $0$ and also the number under a square root must be a positive number. The domain and range can be found out by using graphs also.
Let us plot $y=-1$ on the graph.