Question

What is the domain and range of a line on the x axis?

Answer 1

First of all determine the function $y=f\left( x \right)$ by using the fact that the equation of a line parallel to x axis is given as $y=a$ where $\left| a \right|$ is the distance of the line from the x axis. Substitute the value of a using the given information and draw the graph of the obtained equation. See the possible values of x for which the function is defined to determine the set of domains while see the possible values of y to determine the range of the function.

Complete step-by-step solution:
Here we have been provided with a line on the x axis and we are asked to determine the domain and range of this line. First we need to determine the function $y=f\left( x \right)$.
Now, we know that the equation of a line parallel to x axis is given as $y=a$ where $\left| a \right|$ is the distance of the line from the x axis. Here it is given that the line is on the x axis that means the distance of this line from the x axis is 0, so substituting a = 0 in the equation $y=a$ we get,
$\Rightarrow y=0$
Let us draw the graph of the above function and determine the domain and range of the function, so we have,

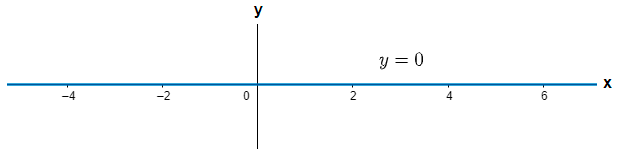
(1) Domain: - Domain of a function is defined as the set of values of x for which the function $y=f\left( x \right)$ is defined. On observing the graph we can see that the values of x extends from $-\infty$ to $\infty$. Therefore, the domain of the function $y=0$ can be given as $x\in \left( -\infty ,\infty \right)$.
(2) Range: - Range of a function $y=f\left( x \right)$ is defined as the set of all the possible values of y for the possible values of x. From the above graph we can see that the only possible value of y is 0 for any real values of x. Therefore, the range of the function $y=0$ can be given as y\in \left\\{ 0 \right\\}.

Note: Note that in the set theory small brackets and square brackets represent the set of values of x in a given interval while the curly bracket represents the particular elements that we want to denote. Here there is only one element in the range that is why we have used the curly bracket. Do not use a square bracket in place of a small bracket in $x\in \left( -\infty ,\infty \right)$ because infinity is not a real number so we are including it in the set. Square bracket is used when we include the boundary point value.