Question

What is the distance of the point $(p,q,r)$ from $x$-axis?

Answer 1

For any point $(x,y,z)$ the distance from the centre $(0,0,0)$ is given as $\sqrt {{x^2} + {y^2} + {z^2}}$ and the distance between $({x_1},{y_1},{z_1}){\text{ and }}({x_2},{y_2},{z_2})$ is given by the formula $\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2} + {{({z_2} - {z_1})}^2}}$ this is called the distance formula.

Complete step-by-step answer:
So here we are given the point whose coordinates are given as $(p,q,r)$ and we need to find its distance from the point given to the $x$-axis. So let us assume that the point is represented by the point $P(p,q,r)$ and now we know that by the distance formula we can be able to find the distance between any two points we are given.
Now let us assume that the two points A and B be $({x_1},{y_1},{z_1}){\text{ and }}({x_2},{y_2},{z_2})$ and then the distance between these two points AB=$\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2} + {{({z_2} - {z_1})}^2}}$
So here we are given that the point P is $(p,q,r)$ so in the graphical form it will be represented as

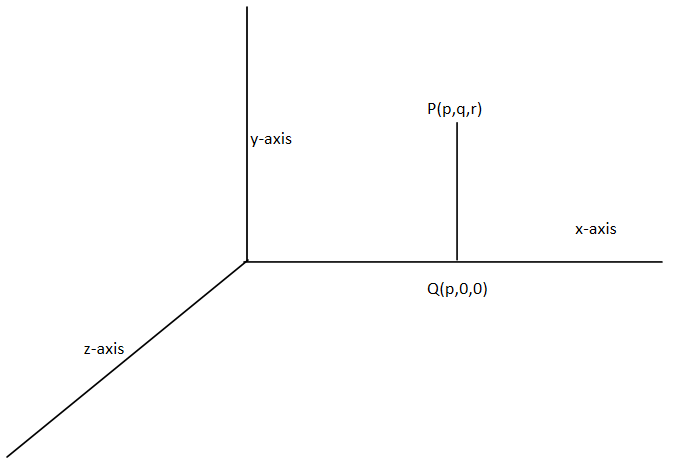
Let us assume that point $Q(p,0,0)$ lies on the x-axis such that PQ is perpendicular to x-axis and we know that the perpendicular distance is the shortest distance therefore we need to find the distance $PQ$ to get the distance between the point P and the x-axis. So here there are two points whose coordinates are known where $P(p,q,r)$ and $Q(p,0,0)$
So here we can apply the distance formula
$PQ = \sqrt {{{(p - p)}^2} + {{(q - 0)}^2} + {{(r - 0)}^2}} \\\ PQ = \sqrt {{{(0)}^2} + {{(q)}^2} + {{(r)}^2}} = \sqrt {{q^2} + {r^2}} \\\$
So we got the distance between the two points as $\sqrt {{q^2} + {r^2}}$

Note: If we are given a line or the plane of the equation $ax + by + cz + d = 0$ and any point $({x_1},{y_1},{z_1})$ lies outside of the plane then the perpendicular distance is given by the formula
$= \left| {\dfrac{{a{x_1} + b{y_1} + c{z_1} + d}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}} \right|$