Question

What is the distance of point (3, 2) from x – axis?

Answer 1

Hint: We have to draw a graph and then mark the point (3, 2) in the Cartesian plane. The distance of a point p (a, b) from x – axis is given by $\left| b \right|$. Similarly take (3, 2) in place of (a, b) and find the distance of point from x – axis.

Complete step by step solution:
The axis of a two – dimensional Cartesian system divides the plane into infinite regions called quadrants each bounded by two half axes.

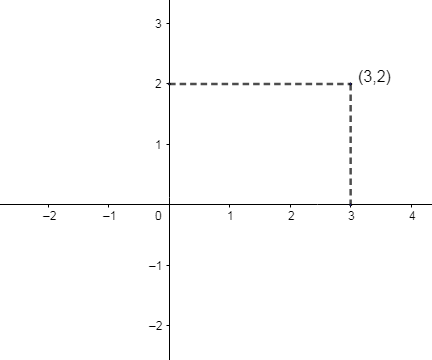
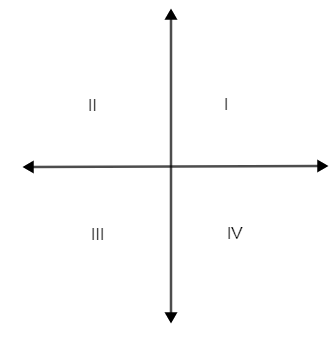
The point (3, 2) is in the quadrant I as both the x – coordinate and y – coordinate is positive.
Thus we can write it as,
x – Coordinate = 3
y – Coordinate = 2
If coordinates of points defined as P (a, b) then the distance of the distance of the point P (a, b) from x- axis is $\left| b \right|$ units.
Let P (a, b) = (3, 2).
Thus the distance of the point P (3, 2) from the x – axis = $\left| 2 \right|$ = 2 units.
Therefore, the distance of the point (3, 2) from the x – axis is 2 units.

Note: If coordinates of the points defined as P (a, b) then the distance of the point P (a, b) from the y – axis is $\left| a \right|$ units. The distance of point (3, 2) from the y – axis is $\left| 3 \right|$ units. The distance of point (3, 2) from the y – axis is $\left| 3 \right|$ units. You might think the distance from the x –axis is the x – coordinates, which leads to the wrong answer. So, don’t get confused.